Биссектриса угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
Соответственно -
Подставим всё то, что нам известно и находим х -
- - -
cм
см.
Квадрат длины биссектрисы угла треугольника равен произведению сторон, из которых выходит биссектриса, без произведения отрезков, на которая она делит третью сторону.
1) Чтобы найти диагональ BD параллелограмма, мы можем использовать теорему Пифагора в треугольнике ABD. Для этого нам нужно найти длину отрезка AD и DC.
Из условия мы знаем, что диагональ AC равна 14 см. Из параллельности плоскости α и диагонали AC следует, что расстояние между прямой AC и плоскостью α равно 6 см. Также известны проекции отрезков AD и DC на плоскость α: √13 см и 2√7 см соответственно.
Для начала найдем длину отрезка AD. Для этого воспользуемся теоремой Пифагора в прямоугольном треугольнике ACD:
AC² = AD² + DC²
14² = AD² + DC²
196 = AD² + DC²
Теперь найдем длину отрезка DC. Для этого воспользуемся данными о проекции отрезка DC на плоскость α:
DC² = (2√7)²
DC² = 28
Подставим это значение в уравнение для длины отрезка AD:
196 = AD² + 28
AD² = 196 - 28
AD² = 168
Теперь найдем длину отрезка AD:
AD = √(168)
AD = 4√(14)
Теперь, используя найденные значения, мы можем найти диагональ BD. Воспользуемся теоремой Пифагора в треугольнике ABD:
BD² = AD² + AB²
BD² = (4√(14))² + AC²
BD² = 16(14) + 14²
BD² = 224 + 196
BD² = 420
BD = √(420)
BD = 2√(105)
Таким образом, диагональ BD параллелограмма равна 2√(105) см.
2) Чтобы найти косинус угла между прямыми AB₁ и A₁D, мы можем использовать формулу для косинуса угла между векторами.
Сначала найдем векторы AB₁ и A₁D. Вектор AB₁ можно найти, вычитая вектор B₁A из вектора AB. Размерность вектора AB₁ будет равна размерности вектора AB:
AB₁ = AB - B₁A
Теперь найдем вектор A₁D, вычитая вектор DA₁ из вектора AD:
A₁D = AD - DA₁
Далее, найдем скалярное произведение векторов AB₁ и A₁D:
AB₁ * A₁D = |AB₁| * |A₁D| * cos(θ)
Здесь |AB₁| и |A₁D| - длины векторов AB₁ и A₁D соответственно, а θ - искомый угол.
Теперь можем выразить косинус угла через найденные векторы:
cos(θ) = (AB₁ * A₁D) / (|AB₁| * |A₁D|)
Вычислим значения для скалярного произведения и длин векторов:
AB₁ * A₁D = AB₁x * A₁Dx + AB₁y * A₁Dy + AB₁z * A₁Dz
где AB₁x, AB₁y, AB₁z - координаты вектора AB₁,
A₁Dx, A₁Dy, A₁Dz - координаты вектора A₁D.
|AB₁| = √(AB₁x² + AB₁y² + AB₁z²)
|A₁D| = √(A₁Dx² + A₁Dy² + A₁Dz²)
Подставим эти значения в формулу для косинуса угла:
cos(θ) = [(AB₁x * A₁Dx + AB₁y * A₁Dy + AB₁z * A₁Dz)] / [(√(AB₁x² + AB₁y² + AB₁z²)) * (√(A₁Dx² + A₁Dy² + A₁Dz²))]
Теперь, чтобы найти значение косинуса угла, подставим известные координаты векторов AB₁ и A₁D и вычислим значение.
3) Чтобы найти геометрическую фигуру, являющуюся параллельной проекции прямых KF и ME на плоскости ACC₁ в направлении прямой BC₁, нужно провести параллельные пересекающиеся прямые через точки F и K. Пересечение этих прямых даст прямую, параллельную BC₁, и являющуюся параллельной проекцией прямых KF и ME на плоскости ACC₁.
Чтобы найти отношение проекций отрезков KF и ME, нужно разделить длину отрезка KF на длину отрезка ME:
отношение = длина KF / длина ME
Вычислить это отношение возможно, когда даны длины самих отрезков КФ и МЕ. Однако, из условия не даны точные значения длин этих отрезков. Чтобы найти эти значения, необходимо дополнительную информацию.
К сожалению, я не могу предоставить чертежи в текстовом формате. Но надеюсь, что объяснения и пошаговые решения помогут вам понять, как решить данные задачи. Если у вас возникнут дополнительные вопросы, не стесняйтесь задавать их.
Дано :
ΔCDE.
СD = 8 см.
DE = 10 см.
СЕ = 12 см.
Отрезок DK - биссектриса ΔCDE.
Найти :
DK = ?
Пусть СК = х, тогда КЕ = 12 (см) - х.
Биссектриса угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.Соответственно -
Подставим всё то, что нам известно и находим х -
- - -
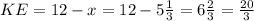 см.
см.
Квадрат длины биссектрисы угла треугольника равен произведению сторон, из которых выходит биссектриса, без произведения отрезков, на которая она делит третью сторону.Запишем в виде формулы -
Осталось только подставить и подсчитать -