1) sin²α=1-cos²α, отсюда sinα=√(1-cos²α)=√1-25/169=√144/169=(-12/13)
sin2α=2sinα*cosα=2*(-12/13)*(-5/13)=120/169.
2) cos2α=cos²α-sin²α=25/169-144/169=(-119/169)
Рассмотрим прямоугольный треугольник MNP. NH - высота, проведённая к гипотенузе, следовательно, она является средним геометрическим для отрезков MH и HP.
Следовательно :
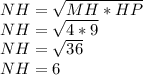
Тогда площадь прямоугольного треугольника MNP равна половине произведения высоты и стороны, к которой проведена эта высота.
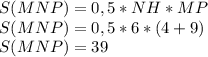
MP - диагональ. Диагональ параллелограмма делит параллелограмм на два равных (в частности и на равновеликих) треугольника. Следовательно, площадь прямоугольника MNPK равна произведению площади треугольника MNP на два.
S(MNPK) = 39*2 = 78.
ответ: 78 (ед^2).
1) Сумма внешнего и внутреннего угла многоугольника равна 180° ⇒ следовательно внутренний угол многоугольника равен 180° - 20° = 160°
Величина внутреннего угла правильного многоугольника зависит от количества его сторон n и выражается формулой:
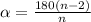
Найдем при каком n угол будет равен 160°:
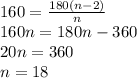
Т.е. угол в 160° будет у правильного 18-угольника
2) Радиус окружности описанной около правильного треугольника R и сторона a треугольника связаны соотношением:
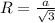
Подставим заданное значение стороны:
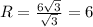
Следовательно, радиус окружности, описанной около этого треугольника равен 6 см
3) Градусная мера всей окружности равна 360°, а радианная мера 2π, следовательно градусная мера дуги равна:
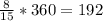 °
°
а радианная:

Длину дуги найдем как 8/15 от длины окружности:
 см
см
sin 2α = 2·sin α·cos α = 2·(±√(1 - cos²α))·cos α = ±2·cos α·√(1 - cos²α) = ±2·(-5/13)·√(1 - (-5/13)²) = ±10/13·12/13 = ±120/169
cos 2α = 2cos²α - 1 = 2·(-5/13)² - 1 = 50/169 - 1 = -119/169