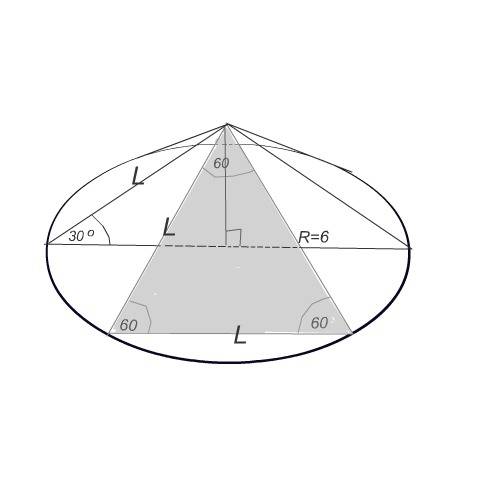
Образующая конуса наклонена к плоскости основания под углом 30°.
Плоскость сечения образована сторонами, равными образующей, и угол между ними 60°
Плоскость сечения - правильный треугольник.
Треугольник, образованный образующей, радиусом конуса и его высотой - половина правильного треугольника.
Высота - катет этого треугольника и равна половине образующей.
Второй катет равен радиусу основания и, как высота правильного треугольника
( можно и по теореме ПИфагора найти), равен (а√3):2=(L√3):2
(L√3):2=6
L√3=12 см
L=12:√3=12√3:√3*√3=12√3:3=4√3 см
Как уже сказано, плоскость сечения - равносторонний треугольник.
Формула площади равностороннего треугольника
S=(a²√3):4
S=(L√3)²√3:4=S=(16 *3)√3:4=48√3:4
S= 12√3 cм²
Площа прямої призми = площа основи*2 + периметр основи*висота.
В основі призми прямокутний трикутник. Його площа = катет1*катет2 /2. Периметр трикутника = сумма всіх сторін. В даному трикутнику відомі дві сторони. За теоремою Піфагора знайдемо гіпотенузу:
6*6+8*8 = 10*10
Гіпотенуза = 10 см
Отже, периметр = 10+6+8 = 24 см
площа = 8*6/2 = 48/2 = 24 кв.см
У прямій призмі бічні ребра перпендикулярні основі, тобто бічне ребро - висота призми.
Тепер площа пр. призми = 2*24 + 24*5 = 48+120 = 168 кв.см
Відповідь: 168 кв.см площа повної поверхні прямої призми.