Фактически задача сводится к нахождению координат вектора CD.
Мы знаем, что СD перпендикулярно AB. И CD проходит через точку C.
Условие перпендикулярности -> косинус угла между векторами CD и AB равен нулю.
Формула косинуса угла между векторами - 
AB={-1+5;4-1}={4;3}
CD={x2-3;y2-2}
Составим уравнение прямой АВ: 
(*)
Подставляя вместо x1 и y1 в формулу косинуса 4 и 3 соответственно получим:
4(x2-3)+3(y2-2)=0
Также точка D принадлежит прямой AB, а значит x2 и y2 удовлетворяют уравнению (*).
Решаем полученную систему уравнений.
Мне лень решать - сами решите. Как найдёте x2 и y2 - подставьте их и найдите координаты вектора CD. Зная координаты направляющего вектора и точку, через которую проходит прямая, легко составить уравнение прямой.
Оно выглядит так: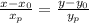 
, где 
- координаты напрвляющего вектора (в нашем случае вектора CD), а х0 и у0 - координаты точки, через которую проходит прямая (в нашем случае С или D - на выбор)
Объяснение:
№6
1) NP = 10 - диаметр => радиус r=10/2 = 5
Рассмотрим ∆ KOP = р/б: OK=OP = r = 5 =>
=> <a = <OKP = 60° Сумма всех углов треугольника = 180° => третий угол равен 180-(60+60) = 60° => ∆KOP - равносторонний, правильный треугольник, и
KP= 5
2) Т.к все эти 3 угла равны между собой, а по рисунку мы видим, что они расположены ровно в половине окружности, т.е их сумма равна 180° =>
3x=180°
x=60° каждый угол. Возвращаясь к 1-вой задачи, мы видим равносторонний правильный треугольник со сторонами 12/2 = 6 => KP= 6.
3) не будем что-то там копать, просто рассмотрим ∆AOC - прямоугольный
по Т.П.: AC=√(16-4)=√12
рассмотрим ∆ ACN - прямоугольный
По Т.П.: AN= √(12+4) = √16 = 4
4) Рассмотрим ∆OAC - прямоугольный
< OAC=30° => по катет напротив угла в 30° равен половине гипотенузы: CO= AO/2 = 6/2 = 3
NC= 6-3 = 3
№9
P= *сумма длин всех сторон*
BN=BK;NK=AP;KC=CP
P= 6+4 + 4+6 + 12 = 32