а) (-2;0) - центр окружности, радиус окружности равен 3.
б) (0; 4) - центр окружности, радиус окружности равен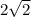 
.
в) (5; -7) - центр окружности, радиус окружности равен 4.
Объяснение:
Уравнение окружности имеет вид: (x-a)²+(y-b)²=R². Здесь центр окружности (a; b) . R - радиус окружности.
а) (-2; 0) -центр окружности, R²=9. R²=3². R=3.
б) (0; 4) - центр окружности,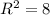 
, 
.
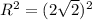
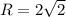в) (5; -7) - центр окружности, R²=16,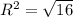 
, R=4.
Заметим, что по условию задачи радиус всегда должен быть положительным. То есть при извлечении корня выбираем только арифметический корень
Виды треугольников: равносторонний, равнобедренный, прямоугольный, остроугольный, тупоугольный.
Равносторонний и равнобедренный - отпадают, т.к. все стороны имеют разную дину.
Определим угол α треугольника, между двумя его меньшими сторонами.
Обозначим стороны: а=3 см, в=15 см, с=17,8 см
По теореме косинусов ∠α=arccos((a²+b²-c²)/2ab)=arccos((9+225-316.84)/2·3·15)=arccos(-82.84/90)≈arccos(-0.92)≈156°
Если ∠α≈156°, то на два остальных угла приходится 180-156=24°, т.е. имеем 1 тупой и 2 острых угла.
Треугольник со сторонами : а=3 см, в=15 см, с=17,8 см - тупоугольный