Найти :Решение :В прямоугольном треугольнике высота, проведённая к гипотенузе - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.
Следовательно,
Площадь прямоугольного треугольника равна половине произведения его катетов.
Следовательно, ед².
ответ :
64 ед².
- - -
70. ABCD - прямоугольник. Найдите .
- - -Дано :
Четырёхугольник ABCD - прямоугольник.
АС - диагональ.
HD⊥АС.
HD = 6, АН = 9.
Найти :
Решение :Прямоугольник - это параллелограмм, все углы которого прямые.
Следовательно ∠D = 90°.
Рассмотрим ΔACD - прямоугольный.
В прямоугольном треугольнике высота, опущенная на гипотенузу - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.
Следовательно,
Площадь треугольника равна половине произведения высоты и стороны, на которую опущена эта высота.
Следовательно, ед².
Диагональ параллелограмма делит параллелограмм на два равновеликих (равных по площади) треугольника.
Точка О-середина оси цилиндра. Диаметр основания цилиндра виден из точки О под прямым углом, а расстояние от точки О до точки окружности основания цилиндра равно 2 см. Вычислите объем цилиндра. Объем цилиндра равен произведению площади его основания на высоту. V=SH Все нужные измерения найдем с т. Пифагора. Точка О - вершина прямого угла равнобедренного прямоугольного треугольника АОВ с катетами АО=ОВ=2 см АВ - гипотенуза этого треугольника=диаметру основания и по т.Пифагора равна 2√2, следовательно, радиус основания цилиндра (2√2):2=√2 СО- половина высоты цилиндра СН и равна радиусу основания, т.к. ОС - медиана треугольника АОВ и по свойству прямоугольного треугольника равна половине АВ, => СО= АС=√2. Высота цилиндра СН =СО*2=2√2 V=SH=π(√2)²*2√2=4π√2 см³
68. По данным на рисунке найдите площадь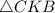 .
.
- - -Дано :ΔСКВ - прямоугольный (∠С = 90°).
СК - высота (СК⊥АВ).
АК = 4, КВ = 16.
Найти :Следовательно,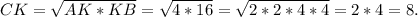
Площадь прямоугольного треугольника равна половине произведения его катетов.Следовательно,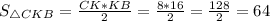 ед².
ед².
ответ :64 ед².
- - -70. ABCD - прямоугольник. Найдите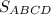 .
.
- - -Дано :Четырёхугольник ABCD - прямоугольник.
АС - диагональ.
HD⊥АС.
HD = 6, АН = 9.
Найти :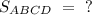
Решение :Прямоугольник - это параллелограмм, все углы которого прямые.Следовательно ∠D = 90°.
Рассмотрим ΔACD - прямоугольный.
В прямоугольном треугольнике высота, опущенная на гипотенузу - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.Следовательно,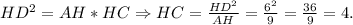
Площадь треугольника равна половине произведения высоты и стороны, на которую опущена эта высота.Следовательно,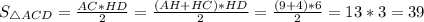 ед².
ед².
Диагональ параллелограмма делит параллелограмм на два равновеликих (равных по площади) треугольника.Тогда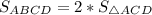 = 2*39 ед² = 78 ед².
= 2*39 ед² = 78 ед².
ответ :78 ед².