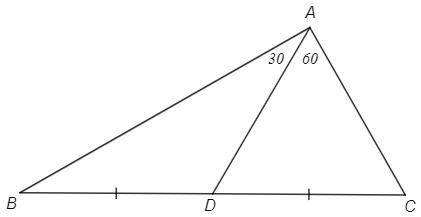
BAC =BAD +CAD =30+60 =90
Медиана из прямого угла равна половине гипотенузы, AD=BD
△ADB - равнобедренный, B=BAD=30
В треугольнике (ABC) с углами 30, 60, 90 стороны относятся как 1:√3:2
AC=AB/√3 =1
----------------------------
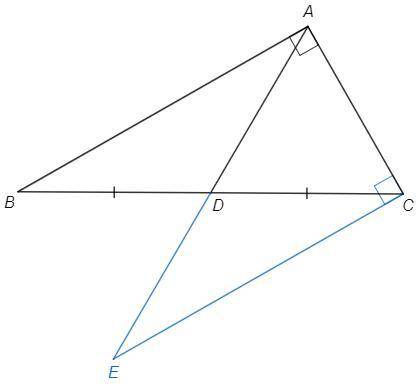
Докажем.
Продлим AD на равный отрезок, DE=AD.
△EDC=△ADB (по двум сторонам и углу между ними)
AB||CE (по накрест лежащим), AB⊥AC => CE⊥AC
△CEA=△ABC (по двум катетам) => AE=BC => AD=DE=BD=DC
(Медиана из прямого угла равна половине гипотенузы.)
△DAC - равносторонний (равнобедренный с углом 60), AC=DC.
(Катет против угла 30 равен половине гипотенузы.)
AC=x, BC=2x
По теореме Пифагора: AB =√(BC^2-AC^2) =x√(4-1) =x√3
AC:AB:BC = 1:√3:2
ab = 28 см; bc = 8 см; cd = 28 см; ad = 8 см.
Объяснение:
1) Пусть am = 2х см, mb = 5 х см.
2) Проведём через точку m прямую, параллельную стороне ad, до пересечения со стороной cd в точке f.
Параллелограмм amfd является ромбом со стороной 2х см, т.к.:
- его стороны попарно параллельны и равны;
- биссектриса угла d является его диагональю, - значит, образовавшаяся фигура amfd является ромбом, и, следовательно,
ad = am = 2х см (как стороны ромба amfd);
bc = ad = 2х см (как противоположные стороны параллелограмма abcd).
3) Таким образом, периметр параллелограмма равен:
(аm + mb) · 2 + ad + bc = (2х + 5х) · 2 + 2х + 2х = 18 х
18 х = 72 см
х = 4 см
3) ab = cd = 7 x = 7 · 4 = 28 см
ad = bc = 2х = 2 · 4 = 8 см
ответ: ab = 28 см; bc = 8 см; cd = 28 см; ad = 8 см.