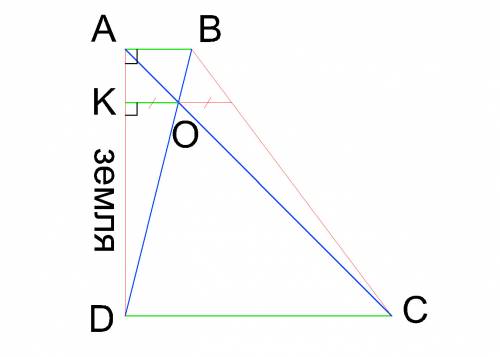
Шесты АВ и ДС как основания образуют прямоугольную трапецию АВСД, а пересечение канатов ВД и СА есть не что иное, как пересечение диагоналей прямоугольной трапеции.
Как известно, отрезок, параллельный основаниям и проходящий через пересечение диагоналей прямоугольной трапеции делится точкой пересечения пополам, и если АВ=х, ДС=у, то длина его равна 2·х·у/(х + у).
Исходя из этого: ОК=2·х·у/(х + у)÷2=х·у/(х + у)
1) ОК=(х·у)÷(х + у)
Как видно, длина ОК никаким образом не зависит от расстояний между шестами, а лишь от их высоты.
2) Если AB=х=2 м, а DC=у=8 м, то ОК=(2·8)÷(2+8)=1,6 м
ответ: длина шеста ОК=1,6 м
Шесты АВ и ДС как основания образуют прямоугольную трапецию АВСД, а пересечение канатов ВД и СА есть не что иное, как пересечение диагоналей прямоугольной трапеции.
Как известно, отрезок, параллельный основаниям и проходящий через пересечение диагоналей прямоугольной трапеции делится точкой пересечения пополам, и если АВ=х, ДС=у, то длина его равна 2·х·у/(х + у).
Исходя из этого: ОК=2·х·у/(х + у)÷2=х·у/(х + у)
1) ОК=(х·у)÷(х + у)
Как видно, длина ОК никаким образом не зависит от расстояний между шестами, а лишь от их высоты.
2) Если AB=х=2 м, а DC=у=8 м, то ОК=(2·8)÷(2+8)=1,6 м
ответ: длина шеста ОК=1,6 м

Прага
Широта: 50°05′16″ с.ш.
Долгота: 14°25′14″ в.д.
Высота над уровнем моря: 202 м
Бангкок
Широта: 13°45′14″ с.ш.
Долгота: 100°30′05″ в.д.
Высота над уровнем моря: 12 м
Магадан
59° 33' 49" (59° 33' 82) северной широты
150° 48' 12" (150° 48' 20) восточной долготы
Сидней
33° 52' 4" (33° 52' 7) южной широты
151° 12' 26" (151° 12' 43) восточной долготы
Чикаго
Широта: 41°51′00″ с.ш.
Долгота: 87°39′00″ з.д.
Высота над уровнем моря: 180 м
P.S. ответы НЕ МОИ. Брала с источников в интернете