35114225 35113996
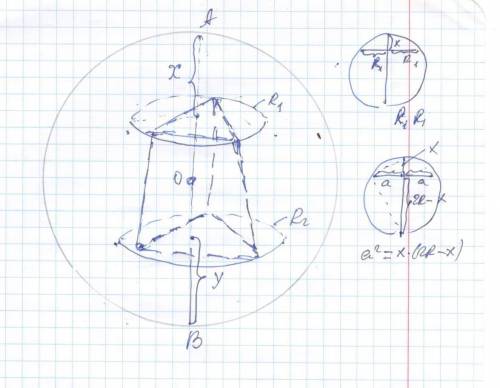
Высота усеченной правильной пирамиды равна 7 см, а длины сторон оснований 3√3 см и 4√3 см. Вычислить радиус описанного шара
R₁ =3√3* √3 /3 = 3 * * * R =(a√3/2)*2/3 =(a√3)/3 * * *
R₂ =4√3* √3 /3 = 4
R₁² = x (2R - x) ⇔x² - 2Rx + 9 = 0 ⇒ x₁ =R -√(R²- 9)
Маленький кусок диаметра x₁ =12 (между основания со стороной 3√3 и поверхностью шара) ( большой кусок x₂=R+√(R²- 9) )
Аналогично
R₂² = y (2R -y) ⇔ y² - 2Ry + 16=0 ⇒ y ₁ = R -√(R²- 16 )
x₁+ H + y₁ = 2R ⇔ R -√(R²- 9) + 7 + R -√(R²- 16) = 2R ⇔
R -√(R²- 9) + 7 + R -√(R²- 16) =2R ;
√(R²- 9) + √(R²- 16) =7 * * * ясно R =5 * * *
примитивное иррациональное уравнение ,необяз. замена t =R² > 0
√(t- 16) = 7 - √(t - 9) ⇔ t- 16 =49 -14√(t - 9) + t -9⇔ 14√(t - 9) =56 ⇔
t - 9 = 4² ⇔ t =25 * * * 3 ; 4 ;5 * * *
R² =25 ⇒ R = 5 ( R = -5 построенное решение )
ответ : 5 см .
угол1 + угол2= 180°-90°=90°
Найдем одну часть: 90°/3= 30°
угол1= 1 часть= 30°
угол2= 2 части= 30°*2= 60°
ответ: угол1=30°; угол2=60°
б)Треугольник равнобедренный, значит угол2= 70°
угол1= 180°-70°-70°= 40°
ответ: угол1=40°; угол2=70°
в)Треугольник прямоугольный, равнобедренный, значит
угол1+угол2=90°
В то же время угол1=угол2=> = 90°/2= 45°
ответ: угол1=45°; угол2=45°
г)угол3= 180°-150°=30°
угол1 + угол2= 180°-30°= 150°
угол2 - угол1= 10°=> угол2= 80°; угол1=70°
ответ: угол1=70°; угол2=80°
д)угол3= 180°-110°= 70°
Тругольник равнобедренный, значит угол1= угол3= 70°
угол2=180°-70°-70°= 40°
ответ: угол1=70°; угол 2=40°
е)угол3= 180°-40°= 140°
угол1 + угол2= 180°-140°= 40°
угол1+угол2= 8 частей( из отношения 5:3)=>
1 часть равна 40°/8= 5°
угол1= 5°*5= 25°
угол2= 5°*3= 15°
ответ: угол1=25°; угол2=15°