50°; 130°; 50°; 130°
Объяснение:
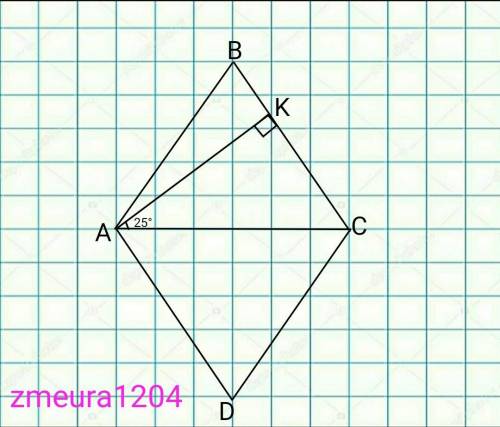
∆AKC- прямоугольный треугольник СК- высота.
Сумма острых углов в прямоугольном треугольнике равна 90°
<КАС+<КСА=90° →
<КСА=90°-<КАС=90°-25°=65°
Диагонали ромба являются биссектриссами углов.(свойство ромба)
<ВCD=2*KCA=2*65°=130°; (АС- биссектрисса угла <ВСD)
Сумма углов прилежащих к одной стороне ромба равна 180°
<ВСD+<ADC=180°, свойство ромба
<АDC=180°-<BCD=180°-130°=50°
Противоположные углы ромба равны.
<АDC=<ABC, свойство ромба
<ВСD=<BAD, свойство ромба
1. По одному из теорем сторон ∆, мы узнаем, что AD=AB-BD=19-9,5=9,5см
DC=BC-BD=19-9,5=9,5см
2. По правилу: катет лежащий напротив угла в 30° равен половине гипотенузы
Находим, что если АD=1/2AB, то угол ABD=30°. То же самое и с ∆BCD.
3. Из правила: сумма острых углов прямоугольного треугольника равна 90°
Находим, что угол ВАС= углу ВСА= 60°
4. Теперь найдем общий угол АВС= АВD+CBD=30+30=60°
5. Это уже дополнительно, но из всего этого можно добавить, что ∆АВС не только равнобедренный, но и равносторонний
6. Также хочу уточнить, что высота ВD разделила ∆АВС на прямоугольные треугольники ∆ ABD и ∆BCD, в которых угол D равен 90°
ОТМЕТЬ, КАК ЛУЧШИЙ ОТВЕТ