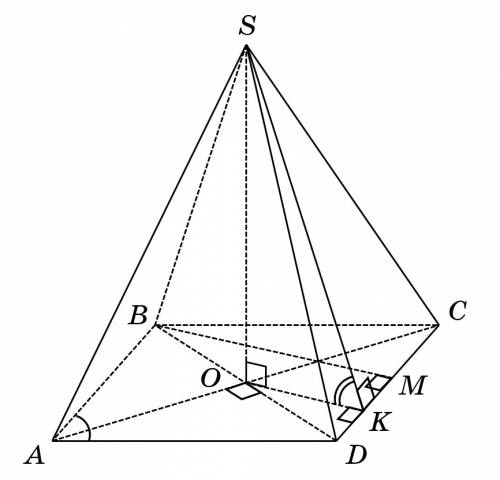
Пусть 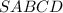 — четырёхугольная пирамида, в основании которой ромб
— четырёхугольная пирамида, в основании которой ромб 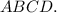 Меньшая диагональ ромба
Меньшая диагональ ромба 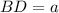 и острый угол
и острый угол 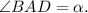
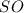 высота пирамиды, значит,
высота пирамиды, значит, 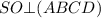 , следовательно
, следовательно 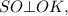 так как
так как 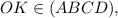
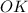 — проекция
— проекция 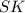 на плоскость
на плоскость 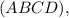
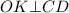 ⇒ по теореме о трёх перпендикуляров (ТТП)
⇒ по теореме о трёх перпендикуляров (ТТП) 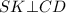 , следовательно,
, следовательно, 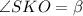 — линейный угол двугранного угла при ребре
— линейный угол двугранного угла при ребре 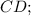 так как все двугранные углы при основании равны, то точка О — центр вписанной окружности, то есть
так как все двугранные углы при основании равны, то точка О — центр вписанной окружности, то есть 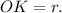
Найти: 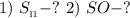
Решение. Ромб 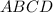 состоит из четырёх равных прямоугольных треугольников:
состоит из четырёх равных прямоугольных треугольников: 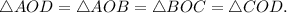
Рассмотрим 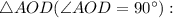
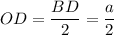
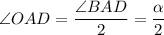
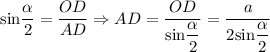
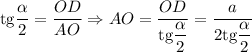
Значит, диагональ 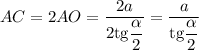
Рассмотрим 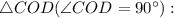
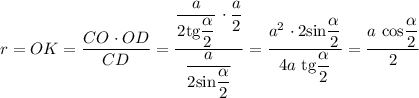
Высота ромба 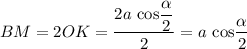
Площадь основания пирамиды 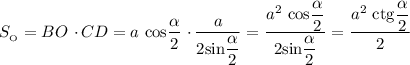
Рассмотрим 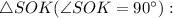
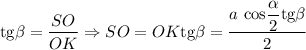
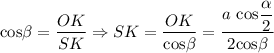
Определим площадь треугольника 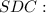
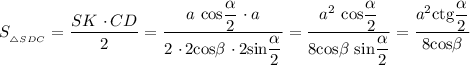
Из-за того, что у ромба все стороны равны и все двугранные углы при основании равны, то все боковые грани пирамиды будут тоже равны. Следовательно, площадь боковой поверхности 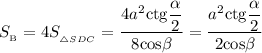
Теперь, зная площадь основания и боковой поверхности пирамиды можно найти площадь полной поверхности:
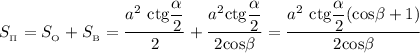
ответ: площадь полной поверхности пирамиды равна 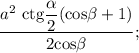 высота пирамиды равна
высота пирамиды равна 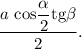
∠ВЕС = 34°.
Объяснение:
Треугольник АВС - равнобедренный. (АВ=ВС) => (∠BAC = ∠BCA).
Тогда ∠DAB = ∠ACF равны как смежные с равными углами.
Треугольники ABD и FCF равны по двум сторонам (AD=AC, AB=CF) и углу между ними (∠DAB = ∠ACF).
В равных треугольниках против равных сторон лежат равные углы. Следовательно, ∠DBA = ∠AFC = 31°, а ∠CAF = ∠BDA = 25°.
∠BCA - внешний угол треугольника АСF и равен сумме двух углов, не смежных с ним, то есть ∠BCA = ∠CAF + ∠CFA = 25+31 = 56°.
∠СВЕ - внешний угол треугольника АВС => ∠СВЕ = ∠BAC + ∠BCA.
∠СВЕ = 56+ 56 = 112°.
Треугольник СВЕ равнобедренный и ∠ВЕС = ∠ЕСВ = (180 - 112/2 = 34° по сумме углов треугольника.
ответ: ∠ВЕС = 34°.