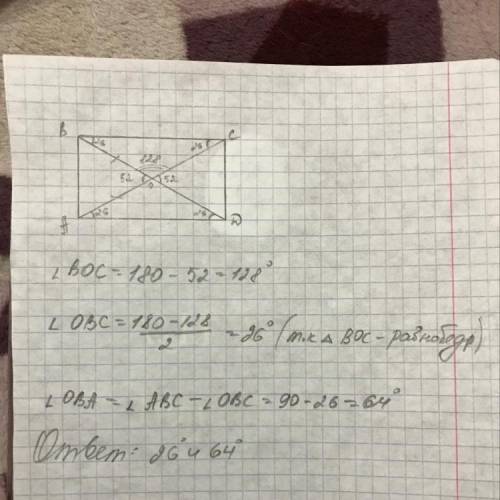
1,3,4,5,6,7,8,9
Объяснение:
1- по двум сторонам и углу между ними,
3- AC-общая ,следовательно по 2-ум сторонам и углу между
4- BD- общая, по 2-ум сторонам и углу между
5- DF-общая, по 2-ум сторонам и углу между
6- Рассмотрим треугольник AHP - он равнобедренный т.к. углы при основании AP равны ,значит треугол. AMP и ANP равны по 2-ум углам у стороне прилежащей к ним
7- NK -общая,значит они равны по трем сторонам
8- BD-общая, они равны о 2-ум углам и стороне между
9- т.к. AD=BF,значит они равны по 2-ум углам и стороне между
∠ АСВ=80°
Так как вписанный угол равен половине угловой меры дуги, на которую он опирается, то ∠АDВ=1180°:2=59° , ∠DBE=42°:2=21°.
Рассмотрим ΔСDВ=, где ∠АDВ=59° , ∠DBE=21°.
Согласно теореме о сумме трёх углов треугольника
∠ DСВ=180°-59°-21°=100°.
∠ DСВ и ∠АСВ- смежные, следовательно
∠АСВ=180°-∠ DСВ =180°-100°=80°
2вариант решения
Так как вписанный угол равен половине угловой меры дуги, на которую он опирается, то ∠АDВ=1180°:2=59° , ∠DBE=42°:2=21°.
Рассмотрим ΔСDВ=, где ∠АDВ=59° , ∠DBE=21°.
∠АСВ- внешний угол треугольника СDB. Внешний угол треугольника равен сумме двух я углов треугольника, не смежных с этим внешним углом :
∠АСВ= ∠АDВ+ ∠DBE=59°+21°=80°.
Диагонали прямоугольника при пересечении образуют 4 равнобедренных треугольника - 2 с углом при вершине 52° и 2 с углом при вершине 180-52=128°. При этом углы при основании этих треугольников являются искомыми в этой задаче (∠В и ∠С).
Угол при основании равнобедренного треугольника равен (180-∠А)/2,
∠А - угол при вершине. ⇒Для первого Δ ∠В= (180-52)/2=64°
Для второго ∠С=(180-128)/2=26°
ответ: 26° и 64°