Каждое ребро правильной шестиугольной призмы равно а. Найдите площадь поверхности призмы.
---
Призма называется правильной, если ее боковые ребра перпендикулярны основаниям, а основания – правильные многоугольники.
Все ребра правильной призмы равны, ⇒
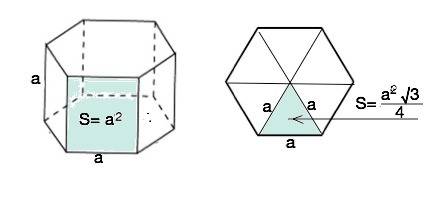
каждая из 6 боковых граней – квадрат, площадь которого S=a².
Ѕ(бок)=6а²
Основания правильной шестиугольной призмы - правильные шестиугольники, состоящие из 6 равных правильных треугольников.
Формула площади правильного треугольника S=(a²√3):4 ⇒
Ѕ (осн)•2=2•6•(a²√3):4=3а²√3
Площадь поверхности призмы равна сумме площадей: площади боковой поверхности и двух оснований.
S (призмы)= 6а²*+3•a²√3 или 3а²•(2+√3) ≈11,2а²
1.
По рисунку a и b не параллельные, поэтому накрестлежащих впринципе нет.Но если предположить, что a || b, то накрестлежащими являются пары углов 2 и 3, 1 и 4.
2.
Искомый и известный углы являются накрестлежащими, а значит равны (110°)
3.
Если угол 1 равен 180-110=70°, то a || b
4.
По 2 признаку (по стороне и прилежащим к ней двум углам)