Столбы ставят перпендикулярно земле, а, следовательно, они параллельны между собой. Таким образом, получим, что ситуация, описанная в задаче, представляет собой следующую задачу:
Дана прямоугольная трапеция АВСD, основания которой BC = 9м и AD = 15м, а боковая сторона СD = 16м. Найдем сторону АВ (см. рис.).
Проведем СМ ⊥ AD, тогда ВС = АМ и АВ = СМ.
Получим прямоугольный треугольник СМD, у которого гипотенуза СD = 16 м, МD = АD - АМ = АD - ВС = 15- 9 = 6 (м).
По теореме Пифагора СМ² = СD² - МD² = 16² - 6² = 256 - 36 = 220 =
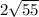
, откуда СМ =
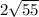
м.
Значит. и АВ =
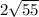
м.
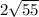
м
а) Векторы не коллинеарны.
б) |2c-3d| = √225 = 15.
Объяснение:
а) Векторы коллинеарны (параллельны), если их соответствующие координаты пропорциональны. Если коэффициент пропорциональности положителен, то векторы сонаправлены.
x =3/-4. y = -2/4 =-1/2. z =-4/-3. Векторы не коллинеарны.
б) Вектор с{6-(-16);-4- 16; -8 -(- 12)} или с{22;-20;4} => 2c{44;-40;8}.
Вектор d{3-(-8);-2-8; -4-(-6)} или d{11;-10;2} => 3d{33;-30;6}.
Вектор(2c-3d) = {11;-10;2} => |2c-3d| = √(121+100+4) = √225 = 15.