ответ: h=5 см .
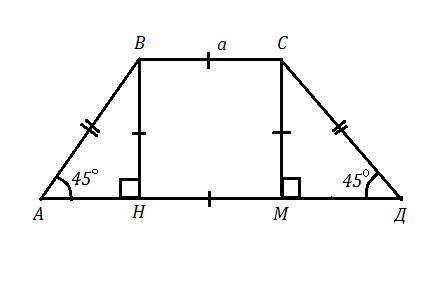
АВСД - трапеция, АВ=СД , ∠А=∠Д=45° ,
ВС=а , ВН ⊥ АД , h=ВН=ВС=а , S(трап)=50см² .
Опусти перпендикуляр из вершины С на АД: СМ ⊥ АД .
Тогда ВСМН - прямоугольник , противоположные стороны которого равны, ВС=МН и ВН=СМ , но так как по условию ВС=ВН, то ВСМН - квадрат, сторону которого обозначим "а" .
ΔАВН - прямоугольный, с углом ∠А=45° . Тогда и ∠АВН=90°-45°=45° .
То есть ΔАВН - равнобедренный и АН=ВН=а .
Аналогично, из ΔСДМ получаем, что ДМ=СМ=а .
Тогда АД=АН+НМ+МД=а+а+а=3а .
Площадь трапеции : 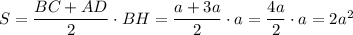
По условию: 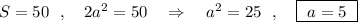
Все грани прямоугольного параллелепипеда - прямоугольники.
Двугранный угол DABD₁ - это угол между плоскостями DAB и ABD₁.
АВ - ребро двугранного угла.
DA⊥AB как стороны квадрата,
DA - проекция наклонной D₁A на плоскость DAB, значит
D₁A⊥АВ по теореме о трех перпендикулярах.
DA⊥AB и D₁A⊥АВ,, значит ∠D₁AD - линейный угол двугранного угла D₁ABD.
ΔADC: ∠ADC = 90°, по теореме Пифагора
AD = √(AC² - CD²) = √(100 - 36) = √64 = 8 дм
ΔD₁AD: ∠D₁DA = 90°, DD₁ = AA₁ = 8√3 дм, AD = 8 дм,
tg∠D₁AD = D₁D / AD = 8√3 / 8 = √3
∠D₁AD = 60°
1. МК = 33 см
2. МК = 3 см.
Объяснение:
1. МВК => MK = 15+18 = 33 cм
2. ВМК => MK = 18 - 15 = 3 см.