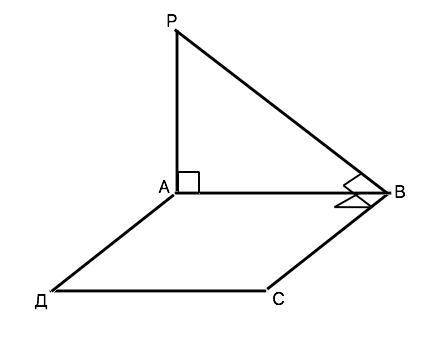
РА - перпендикуляр к площади параллелограмма АВСД. Укажите вид параллелограмма, если РВ перпендикулярен ВС. а) ромб, б) прямоугольник; в) квадрат.
Объяснение: РВ - наклонная. АВ - её проекция на плоскость АВСД. По т. о 3-х перпендикулярах если наклонная (РВ) перпендикулярна прямой (ВС) на плоскости, то её проекция на ту же плоскость перпендикулярна данной прямой. Следовательно, АВ⊥ВС, и угол АВС - прямой. Противоположные углы параллелограмма равны. ⇒ ∠Д=∠В=90°, поэтому из суммы углов четырехугольника ∠А+∠С=360°-2•90°=180°, и каждый из них равен 180°:2=90°.
Углы четырехугольника АВСД прямые. ⇒ АВСД - прямоугольник. Он может быть и квадратом. если его стороны будут равны.
где вы эти условия берете, непонятно.
Если провести сечение пирамиды (очень правильной и совершенно четырехугольной) через точки на двух соседних сторонах квадрата, лежащего в основании, и точку на боковом ребре, НЕ имеющем общих концов с теми двумя сторонами основания, то получится пятиугольник.
И даже не надо доказывать строго, что в общем случае он неправильный. :(((
Дело в том, что, если одну из точек на стороне основания приближать вдоль стороны к вершине квадрата (той, которая не принадлежит той стороне, на которой вторая точка на основании), то одна из сторон стягивается в точку, и когда точка на сечении совпадает с вершиной, пятиугольник превращается в четырехугольник. Который уж никак не может иметь свойства правильного пятиугольника.
Так что задача неверная. Может, условие какое-то другое?