Избавься от ограничений
ПОПРОБУЙ ЗНАНИЯ ПЛЮС СЕГОДНЯ
petruk66
29.03.2020
Геометрия
5 - 9 классы
ответ дан
1.Як називають точку рівновіддалену від усіх точок кола: вершиною чи центром?2. Як називають відстань від точки кола до його центра:перпендикуляром чи радіусом?
3.Як називають хорду, яка проходить через центр кола :діагональ чи діаметр?
4. Діаметр кола дорівнює 8см. Чи будь-який радіус кола дорівнює 4см?
5. Скільки спільних точок можуть мати коло і пряма?
6. Скільки спільних точок можуть мати два кола?
7. Що більше:відстань від центра кола до дотичної чи радіус кола?
8. Скільки різних дотичних до кола можуть провести через точку, що лежить поза колом?
1
СМОТРЕТЬ ОТВЕТ
Войди чтобы добавить комментарий
ответ
3,6/5
9

LymarIvan
почетный грамотей
717 ответов
485.8 тыс. пользователей, получивших
1. центр
2. радіус
3. діаметр
4. так, бо r=D/2
5. жодну, одну або дві
6. жодну, одну або дві
7. радіус кола, проведений в точку дотику, перпендикулярний до дотичної, а довжина цього перпендикуляра якраз є відстанню між точкою (центром) і прямою (дотичною), тобто дорівнює радіусу отже, вони рівні
8. дві
вроде так
это из знания .ком
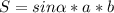
![S=[tex] \frac{1}{2}](/tpl/images/0845/6175/2cd8a.png) *12*20=120см²
*12*20=120см²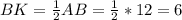
Чтобы доказать, что линия AR перпендикулярна плоскости MNPQ, мы можем воспользоваться свойством параллелограмма и треугольника.
Обратимся к треугольнику AMQ. Поскольку M и N являются серединами сторон AB и BC соответственно, то отрезок MN параллелен и равен половине отрезка AC. А по свойству параллелограмма, диагонали параллелограмма делятся пополам. Таким образом, точка R, являющаяся точкой пересечения отрезков MQ и NP, является серединой отрезка AC.
Аналогичные рассуждения можно провести для треугольников BNP, CPM и DQN, и прийти к выводу, что точка R является серединой отрезков BD, CD и AD соответственно.
Таким образом, линия AR проходит через середины всех ребер тетраэдра ABCD, а значит, она является медианой этого тетраэдра. Поскольку медиана пересекает плоскость MNPQ в ее центре (точке пересечения медиан), то линия AR будет перпендикулярна этой плоскости.
Таким образом, мы доказали, что линия AR перпендикулярна плоскости MNPQ.