Сначала немного теории. Тут у нас импликация(если..то...), комбинированная с конъюнкцией(и). Таблица истинности импликации(стрелочки): 0 0 1 0 1 1 1 0 0 1 1 1 Общее правило: если a<=b, тогда правда Таблица истинности конъюнкции(/\): 0 0 0 0 1 0 1 0 0 1 1 1 Общее правило: если есть одна ложь-всё ложь Теперь о примере: Просто подставляем вместо x варианты. Так как между двумя скобочками с Если... То... стоит И, нам нужен вариант, где оба Если... То... являются правдой. Рассмотрим подробно 1 вариант: 21<25 - это правда 21<23 - это правда Таким образом, в первых скобочках правда, это доказывает таблица истинности, приведённая выше. 21<22 - это правда 21>21 - это ложь В этих скобочках-ложь. А так как ложь и правда в И являются ложью, нам не подходит данный вариант 2 вариант-верный ответ, т.к.: 22<25 - это правда 22<23 - это правда В первых скобочках правда 22<22 - это ложь 22>21 - это правда И в этих скобках правда. Как можно убедится, снова взглянув в таблицу истинности для конъюнкции, всё выражение является правдой. 3 и 4 посмотрите сами и убедитесь что это ложь.
должно быть минимум 7 элементов
Объяснение:
Каждый излучающий элемент имеет два состояния- красный или синий цвет (выключенное состояние не рассматривается по условиям).
Значит, число возможных вариантов, которые можно показать на таком табло равно двум в степени, равной числу элементов.
Например:
один элемент: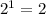 различных сигнала (состояния панели)
различных сигнала (состояния панели)
три элемента: различных сигналов можно отобразить
различных сигналов можно отобразить
шесть элементов: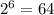 различных сигнала (мало, надо сто)
различных сигнала (мало, надо сто)
семь элементов: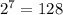 различных сигналов (нам хватит)
различных сигналов (нам хватит)
Выбираем семь элементов, т.к. ими можно отобразить сто вариантов (и даже немного больше).
Можно и посчитать число элементов напрямую, без подбора.
Считается через логарифм по основанию два из десяти, затем округляется с избытком (то есть, всегда вверх):
В расчёте также показано, что такой логарифм можно посчитать через отношение двух десятичных логарифмов (lg), либо двух натуральных логарифмов (ln).