Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 7 раз
Сместиться на (−3,−2) Сместиться на (2,2) Сместиться на (3,9 )
конец
Какую команду надо выполнить Чертёжнику, чтобы вернуться в исходную точку, из которой он начал движение?
ответ: Сместиться на (x−ответ,y-ответ
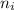вершин, то общее число рёбер будет суммой по всем компонентам связности: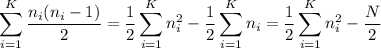
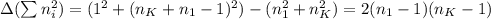
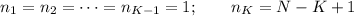
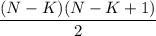
2. integer
3. sqrt(число)
4. var
5. 16
6. 2
7.
function x(a,b,c:integer);
begin
x:=-b+sqr(b)-sqr(4*a*c)*a;
end;
8. 11
9. end.
10. d)
11.
var a,b,c:integer;
result:real;
begin
readln(a,b,c);
result:=(a*b*c)/3;
writeln(result:0:3);
end.
12. real
13. оператор присвоения
14. Присвоить переменной F значение 125
15. write(B); или writeln(B);
16. корень из суммы квадрата х и ста делить на разность а и b умноженной на с
17. с)
18. Нет картинки как образован массив, значит сами решите
19. d)
20. c)
21. c)