На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город К?
Исходный код программы, выполнявшей вычисления (С++) дан во вложении.
UPD: Выше был также представлен алгоритм рекурсивного обхода. Автор вводит как количество доехать из города A в город X. Посмотрим на город К. В него можно приехать из городов И, Ж, Е и Л. Таким образом, Nк = Nи + Nж + Nе + Nл. В свою очередь, в город И можно приехать только из города Д, значит, Nи = Nд, Nд = Nб + Nв и так далее до города А, для которого Nа = 1.
Если я правильно понял то 1024 цвета, может содержать 1 пиксел.Если так то начнём: 1024 =2^10 цвета можно закодировать 10 битами. то есть на 1 пиксель отводится 10 бит. Потом считаем сколько пикселей находится в нашем изображении: это получается 200*150=30000 пикселей. Умнажаем кол-во пикселей на размер памяти которой надо для 1 пикселя: 30000*10=300000 бит. осталось перевести это в кбайты. 1 байт=8 бит 1кбайт=1024байта 1кбайт=1024*8=8192бита потом делим 300000бит на 8192 и получается 36.6 или приблизительно 37 кбайт
var a,b,c:integer; begin read(a,b,c); if (a > b) and (a > c) then write(a) else if (b > a) and (b > c) then write(b) else write(c); end. В делфи добавишь на форму Эдиты(4 штуки) и одну кнопку. В трех Эдитах будешь вводить свои значения, а в четвертом выведешь ответ и все это при клике на кнопку: Procedure btn1Click; var a, b, c, max: integer; begin a:= StrToInt(edt1.Text); // где edt1,2,3 - имена полей для ввода(Эдиты) b:= StrToInt(edt2.Text); c:= StrToInt(edt2.Text); if (a > b) and (a > c) then max:= a; else if (b > a) and (b > c) then max:= b; else max:= c; edt4.Text:= 'Максимальное число' + max; //или ShowMessage(Максимальное число' + max); end.
17
Объяснение:
АБВДЖК, АБВДИК, АБВЕЖК, АБВЕК, АБВЕЛК, АБВЖК, АБДЖК, АБДИК, АГВДЖК, АГВДИК, АГВЕЖК, АГВЕК, АГВЕЛК, АГВЖК, АГЕЖК, АГЕК, АГЕЛК.
Исходный код программы, выполнявшей вычисления (С++) дан во вложении.
UPD: Выше был также представлен алгоритм рекурсивного обхода. Автор вводит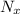 как количество доехать из города A в город X. Посмотрим на город К. В него можно приехать из городов И, Ж, Е и Л. Таким образом, Nк = Nи + Nж + Nе + Nл. В свою очередь, в город И можно приехать только из города Д, значит, Nи = Nд, Nд = Nб + Nв и так далее до города А, для которого Nа = 1.
как количество доехать из города A в город X. Посмотрим на город К. В него можно приехать из городов И, Ж, Е и Л. Таким образом, Nк = Nи + Nж + Nе + Nл. В свою очередь, в город И можно приехать только из города Д, значит, Nи = Nд, Nд = Nб + Nв и так далее до города А, для которого Nа = 1.