2.Так как 1 символ вести 5 бит, значит N = 32. (используем формулу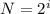 
3. Тут наоборот дано N, а найти i. Опять же пользуемся формулой
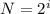и получаем, что 1 символ весит 3 бита.
def translate(inp: str, to: str):
if to == "dobosovski" :
return inp.replace("0", "A").replace("1", "B")
elif to == "feimosovski":
return inp.replace("A", "0").replace("B", "1")
return inp
print("перевод на добосовский: ")
dres = translate(input(), "dobosovski")
print("результат >>", dres)
print("перевод на феймосовский: ")
fres = translate(input(), "feimosovski")
print("результат >>", fres)
Объяснение:
функция translate принимает 2 параметра: inp и to
inp - строка, которую нужно перевести
to - на какой язык
если to == dobosovski, то меняем 0 на A, 1 на B
если to == feimosovski, A на 0, B на 1
если to не равен ни feimosovski, ни dobosovski - вернем строку, которую нужно перевести
Агрегація — термін, який має кілька значень. Ця сторінка значень містить посилання на статті про кожне з них.
Якщо ви потрапили сюди за внутрішнім посиланням, будь ласка, поверніться та виправте його так, щоб воно вказувало безпосередньо на потрібну статтю.
Агрега́ція або агрегува́ння (лат. aggregatio «приєднання») — процес об'єднання елементів в одну систему. Агрегація у хімії, збагаченні корисних копалин тощо — злипання частинок у багатокомпонентний утвір — агрегат. Результат агрегатування.
Агрегація у програмуванні — це вид композиції.
Агрегація формених елементів крові у медицині при різних патологічних станах, часто при тромбозах.
Агрегація (англ. Aggregation) у статистиці – об'єднання пов'язаних категорій, зазвичай в рамках загальної гілки ієрархії, що служить для надання інформації в більш широкому контексті, ніж той, в якому збираються докладні дан .[1]
Агрегування (нейронні мережі) — нелінійне зниження дискретизації шару штучної нейронної мережі.
2. 32 символа.
3. 3 битам.
Объяснение:
2) Чтобы узнать мощность алфавита достаточно вес одного символа преобразовать в степень двойки. 2^5 = 32 - мощность алфавита.
3) Чтобы узнать вес одного символа нужно воспользоваться формулой Хартли: N = 2^i, где i - это вес одного символа. В данной задаче N - это восемь. 8 = 2^3.