
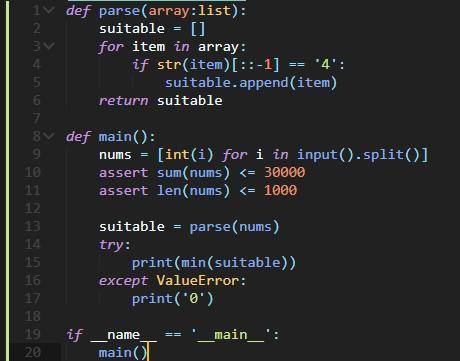
def parse(array:list):
suitable = []
for item in array:
if str(item)[::-1] == '4':
suitable.append(item)
return suitable
def main():
nums = [int(i) for i in input().split()]
assert sum(nums) <= 30000
assert len(nums) <= 1000
suitable = parse(nums)
try:
print(min(suitable))
except ValueError:
print('0')
if __name__ == '__main__':
main()
Объяснение:
Сайт гарантированно сломает код, по скриншоту его можно восстановить.
Принцип работы:
Получаем на вход список чисел
Утверждение - сумма всех элементов меньше 30 000
Утверждение - всего в списке не более 1000 элементов
Если одно из утверждений не верно, программа завершает работу с ошибкой AssertionError (Ошибка утверждения)
Прогоняем список через функцию parse, результат сохраняем в переменную suitable (подходящие)
Пытаемся вывести на экран минимальный элемент списка suitable.
Если список пуст, будет возбуждено исключение ValueError, перехватываем его, вместе ошибки выводим в консоль 0
Функция Parse: <= Список
Локальная переменная suitable типа list (список)
Для каждого элемента списка, переданного функции -
Если последний символ в строковом представлении элемента списка есть 4 - добавляем в список suitable, иначе - пропускаем итерацию
Возвращаем список suitable
1321
Объяснение:
Число 2^900 в двоичном виде - это единица с девятьюстами нулями.
Число 7 - это 2^2+2^1+2^0
2^900-2^0=2^900-1=2^899 (в двоичном виде - это 900 единиц)
2^2+2+1 в двоичном виде выглядит как 110.
Операция 2^899-2^2-2^1 в двоичном виде представляет из себя замену предпоследних, 898-й и 899-й единиц на 0. Число в двоичном виде будет выглядеть как 897 единиц, затем два нуля, затем единица.
Значащих нулей в числе 2^900-7 рано двум.
8^740=(2^3)^740=2^(740*3)=2^2220
Число 2^2220 в двоичном виде - это единица с двумя тысячами двести двадцатью нулями.
2220-900+1=1321 То есть при сложении, число 2^900-7 записывается в числе 2^2220 начиная с 1321-го разряда.
Искомое число 8^740+2^900-7 в двоичном виде будет выглядеть как единица, 1319 нулей, 897 единиц, два нуля и одна единица.
Число значащих нулей в этом числе составит 1319+2=1321.