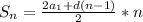
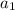 - это член последовательности с индексом 1, то есть первое число в ряду.
- это член последовательности с индексом 1, то есть первое число в ряду.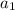 = 1 (в условии задачи сказано что первый подарок весит 1кг)
= 1 (в условии задачи сказано что первый подарок весит 1кг)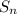 - это сумма веса всех подарков, в примере используется слово "weight" что в переводе "вес", поэтому подставим это слово.
- это сумма веса всех подарков, в примере используется слово "weight" что в переводе "вес", поэтому подставим это слово.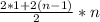
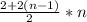
! инверсия значения
& побитовое И
^ исключающее ИЛИ
| побитовое ИЛИ
7(10) = 00111(2)
11(10) = 01011(2)
21(10) = 10101(2)
25(10) = 11001(2)
31(10) = 11111(2)
11 & 7 = 01011 & 00111 = 00011
11 & !7 = 01011 & 11000 = 01000
11 & 7 | 11 & !7 = 00011 | 01000 = 01011
11 & 7 = 01011 & 00111 = 00011
!11 & 7 = 10100 & 00111 = 00100
11 & 7 | !11 & 7 = 00011 | 00100 = 00111
7 & 31 = 00111 & 11111 = 00111
(7 & 31 | (11 & 7 | !11 & 7)) = 00111 | 00111 = 00111
25 & 31 = 11001 & 11111 = 11001
25 | 25 & 31 = 11001 | 11001 = 11001
(7 & 31 | (11 & 7 | !11 & 7)) & (25 | 25 & 31) = 00111 & 11001 = 00001
31^(11 & 7 | 11 & !7) = 11111 ^ 01011 = 10100
31^(11 & 7 | 11 & !7) ^ 21 = 10100 ^ 10101 = 00001
(7 & 31 | (11 & 7 | !11 & 7)) & (25 | 25 & 31) ^ 21 = 00001 ^ 10101 = 10100
31^(11 & 7 | 11 & !7) ^ 21 | (7 & 31 | (11 & 7 | !11 & 7)) & (25 | 25 & 31) ^ 21 =
00001 | 10100 = 10101
10101(2) = 21(10)