Некоторый алгоритм из одной цепочки символов получает новую цепочку следующим образом. Сначала вычисляется длина исходной цепочки символов; если она нечётна, то удаляется первый символ цепочки, а если чётна, то в середину цепочки добавляется символ А. В полученной цепочке символов каждая буква заменяется буквой, следующей за ней в русском алфавите (А - на Б, Б - на В и т. д., а Я - на А). Получившаяся таким образом цепочка является результатом работы алгоритма. Например, если исходной была цепочка РУКА, то результатом работы алгоритма будет цепочка СФБЛБ, а если исходной была цепочка СОН, то результатом работы алгоритма будет цепочка ПО.

Дана цепочка символов ПРУД. Какая цепочка символов получится, если к данной цепочке применить описанный алгоритм дважды (т. е. применить алгоритм к данной цепочке, а затем к результату вновь применить алгоритм)?
Русский алфавит: .

👇

Открыть все ответы

Ответ:

dashanovikova03

02.07.2020

Переводим число из двоичной системы в десятичную:
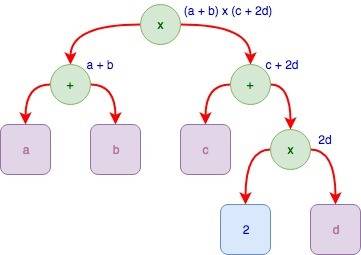
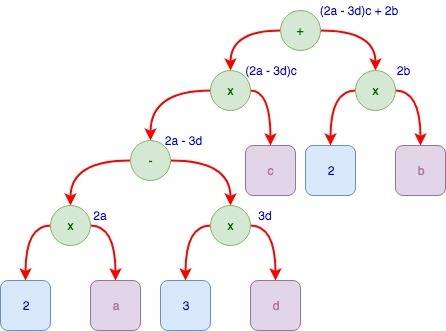
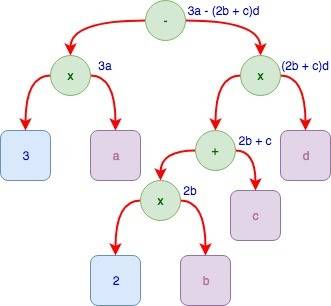
10(2) = 1 * 2^1 + 0 * 2^0 = 2 + 0 = 2

10(2) + 10(10) = 2(10) + 10(10) = 12(10)

Чтобы перевести число из системы счисления с основанием b, можно представить его в виде суммы:
$(\overline{a_n\dots a_2a_1a_0})_b=a_nb^n+\dots+a_2b^2+a_1b^1+a_0b^0$
Всё точно так же, как и в десятичной системе, только меняем 10 на основание системы счисления, например,
$121_{10}=1\cdot10^2+2\cdot10^1+1\cdot10^0=1\cdot100+2\cdot10+1\cdot1\\
121_{4}=1\cdot4^2+2\cdot4^1+1\cdot4^0=1\cdot16+2\cdot4+1\cdot1\\
121_{b}=1\cdot b^2+2\cdot b^1+1\cdot b^0$
Другой избежать большого количества возведений в степень и записать, например, так:
$121_{b}=(((1)b+2)b+1)$
Берем первую цифру – умножаем на b, прибавляем вторую цифру – умножаем на b, прибавляем третью цифру – ... – умножаем на b, прибавляем последнюю цифру.

Чтобы перевести из десятичной в систему с основанием b, нужно по сути сделать в обратном порядке то, что написано выше: либо восстановить разложение в сумму, либо выписать остатки от деления на b в обратном порядке. Например, переведем 27(4) в десятичную систему счисления:
27(4) = 1 * 16 + 2 * 4 + 3 * 1 = 1 * 4^2 + 2 * 4^1 + 3 * 4^0 = 123(4)

27 : 4 = 6 (ост. 3)
6 : 4 = 1 (ост. 2)
1 : 4 = 0 (ост. 1)
Выписываем в обратном порядке: 27(10) = 123(4)

4,6(94 оценок)

Ответ:

snezhanashikolai

02.07.2020

Деревья строятся просто: добавляем узел – операцию, которая выполняется последней, и к ней два потомка – аргументы этой операции. Например, для выражения a + b операцией будет "+", а аргументами – a и b. Затем в таком же виде представляем аргументы этой операции, пока все аргументы не будут содержать выражений. Построенные деревья во вложении.

Префиксная форма записи заключается в том, что сначала записывается операция, потом префиксная запись её первого аргумента, потом второго аргумента. Это соответствует обходу дерева сверху вниз и слева направо, записываем, что сверху, потом идем вниз. Вот что получится в итоге:
а) * + a b + c * 2 d
б) + * - * 2 a * 3 d c * 2 b
в) - * 3 a * + * 2 b c d

В постфиксной записи, наоборот, записываются сначала аргументы, потом операция. Это соответствует обходу дерева снизу-вверх.
а) a b + c 2 d * + *
б) 2 a * 3 d * - c * 2 b * +
в) 3 a * 2 b * c + d * -
Постройте дерево, соответствующее арифметическому выражению. запишите это выражения в префиксной и п