Принцип работы рекурсивный
Объяснение:
# В комментариях я использовал слово итерация в значении запуска новой функции с данными spos/ppos большими на 1 (аналогично с циклом for
# Ввод данных
s = input("Слово: ")
p = input("Шаблон: ")
# match возвращает True, если подстрока s, начинающаяся с позиции spos,
# соответствует шаблону (подстрока p, которая начинается
# с позиции ppos)
def match(spos, ppos):
if (spos == len(s)) or (ppos == len(p)):
return (spos == len(s) and ppos == len(p)) #когда все символы слова либо шаблона пройдены возвращается True, если и шаблон и слово пройдены полностью, в другом случае возвращается False
elif p[ppos] == '?':
return match(spos + 1, ppos + 1) #когда встречается ? начинается новая итерация
elif p[ppos] == '*': #проверка если подстрока - *
for i in range(spos, len(s)): #обход всех оставшихся символов слова
if match(i, ppos + 1):
return True #если дочерняя функция (вызванная выше) выдала True, цикл for заканчивается до выдавая True
else: #выполняется когда не встретилось */?
return (s[spos] == p[ppos]) and (match(spos + 1, ppos + 1))# проверка на равентсво соответствующих (по индексу) символов слова и шаблона и запуск новой функции (итерации)
if match(0, 0):
print('YES') #если результат функции True в консоль выводится 'YES', иначе 'NO'
else:
print('NO')
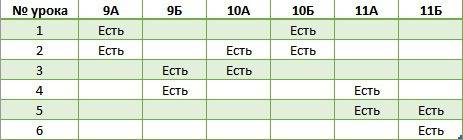
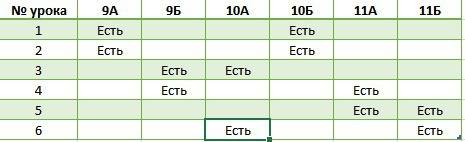
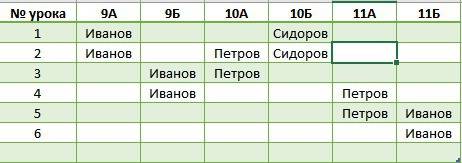
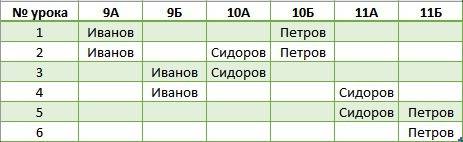
1) А ⋀ В ⋀ С ⋁ А ⋀ ¬В ⋀ С ⋁ А ⋀ В ⋀ ¬С ⋀ D = (А ⋁ А) ⋀ (А ⋁ В) ⋀ (А ⋁ С) ⋀ (¬В ⋁ А) ⋀ (¬В ⋁ В) ⋀ (¬В ⋁ С) ⋀ (С ⋁ А) ⋀ (С ⋁ В) ⋀ (С ⋁ С) ⋁ А ⋀ В ⋀ ¬С ⋀ D = А ⋀ (А ⋁ В) ⋀ (А ⋁ С) ⋀ (¬В ⋁ А) ⋀ 1 (¬В ⋁ С) ⋀ (С ⋁ В) ⋀ С ⋁ А ⋀ В ⋀ ¬С ⋀ D = А ⋀ С ⋁ А ⋀ В ⋀ ¬С ⋀ D =
= (А ⋁ А) ⋀ (А ⋁ В) ⋀ (А ⋁ ¬ С) ⋀ (А ⋁ D) ⋀ (С ⋁ А) ⋀ (С ⋁ В) ⋀ (C ⋁ ¬C) ⋀ (C ⋁ D) =
= A ⋀ (А ⋁ В) ⋀ (А ⋁ ¬ С) ⋀ (А ⋁ D) ⋀ (С ⋁ А) ⋀ (С ⋁ В) ⋀ 1 ⋀ (C ⋁ D) =
= A ⋀ (С ⋁ В) ⋀ (C ⋁ D) = A ⋀ С ⋀ (B ⋁ D)
2) А ⋁ В ⋁ ¬ B ⋀ C ⋀ D ⋁ ¬ B ⋀ ¬ C ⋀ ¬ D ⋁ ¬ B ⋀ C ⋀ D = А ⋁ В ⋁ ¬ B ⋀ C ⋀ D ⋁ ¬ B ⋀ ¬ C ⋀ ¬ D = А ⋁ В ⋁ C ⋀ D ⋁ ¬ B ⋀ ¬ C ⋀ ¬ D = А ⋁ В ⋁ C ⋀ D ⋁ ¬ C ⋀ ¬ D = А ⋁ В ⋁ С ⟷D
3) А ⋀ В ⋀ С ⋁ А ⋀ В ⋀ ¬С ⋁ (A ⋀ ¬B ⋀ C ⋀ D) ⋁ (A ⋀ B ⋀ C ⋀ ¬D) ⋁ (A ⋀ B ⋀ C ⋀ D) = А ⋀ В ⋁ (A ⋀ C ⋀ D) ⋁ (A ⋀ B ⋀ C ⋀ ¬D) = A ⋀ B ⋁ (A ⋀ C ⋀ D) = A ⋀ (B ⋁ C) ⋀ (B ⋁ D) = A ⋀ (B ⋁ C ⋀ D)