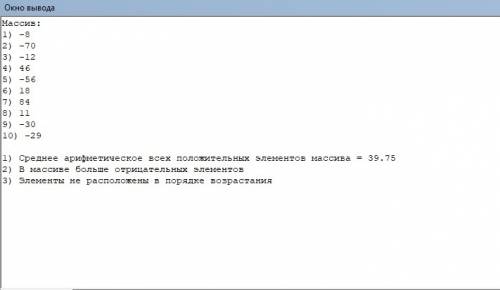
//Я так понял, что под порядком "неубывания" вы имеете ввиду порядок возрастания...
//Поскольку вы не указали исходный массив, я его сгенерировал, а также вывел на экран, чтобы можно было проверить результаты
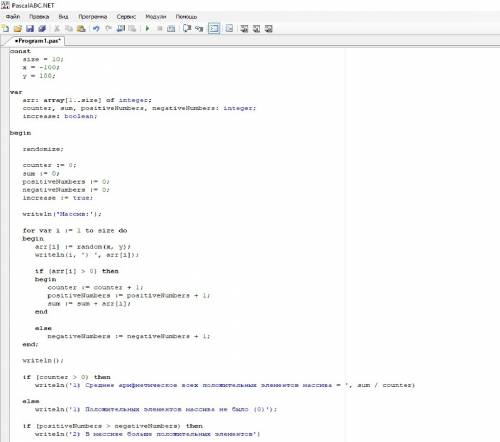
const
size = 10;
x = -100;
y = 100;
var
arr: array[1..size] of integer;
counter, sum, positiveNumbers, negativeNumbers: integer;
increase: boolean;
begin
randomize;
counter := 0;
sum := 0;
positiveNumbers := 0;
negativeNumbers := 0;
increase := true;
writeln('Массив:');
for var i := 1 to size do
begin
arr[i] := random(x, y);
writeln(i, ') ', arr[i]);
if (arr[i] > 0) then
begin
counter := counter + 1;
positiveNumbers := positiveNumbers + 1;
sum := sum + arr[i];
end
else
negativeNumbers := negativeNumbers + 1;
end;
writeln();
if (counter > 0) then
writeln('1) Среднее арифметическое всех положительных элементов массива = ', sum / counter)
else
writeln('1) Положительных элементов массива не было (0)');
if (positiveNumbers > negativeNumbers) then
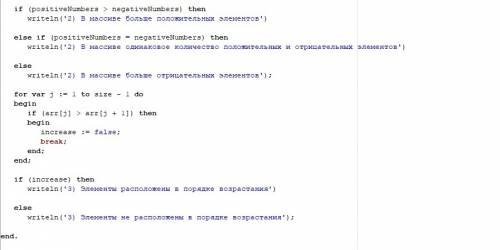
writeln('2) В массиве больше положительных элементов')
else if (positiveNumbers = negativeNumbers) then
writeln('2) В массиве одинаковое количество положительных и отрицательных элементов')
else
writeln('2) В массиве больше отрицательных элементов');
for var j := 1 to size - 1 do
begin
if (arr[j] > arr[j + 1]) then
begin
increase := false;
break;
end;
end;
if (increase) then
writeln('3) Элементы расположены в порядке возрастания')
else
writeln('3) Элементы не расположены в порядке возрастания');
end.
1. 1) 2. 4)
Объяснение:
1. У нас есть таблица истинности.
Берём каждое выражение и сверяем его с таблицей.
1 -истина ; 0 - ложь
\/ - дизъюнкция(логическое сложение) - При сложении 1 и 1, 1 и 0, 0 и 1 получается всегда Истинна. Ложь только в случае сложения 0 и 0.
/\ - конъюнкция (логическое умножение) - При умножении будет истинна только в случае 1 /\ 1 , во всех остальных случаях - Ложь.
Берём первое выражение: X \/ ¬Y \/ Z (Х + (отрицание от Y) + Z
Подставляем значения из таблицы, каждую строчку.
1) 1 1 1 1 : 1 + 0 + 1 = 1 - верно, значит выражение к первой строчке таблицы подходит. Можно заметить, что в таблице X - всегда = 1 и в выражении, оно стоит без отрицания, значит можно сделать вывод, что выражение всегда будет истинно, что и показано в таблице ⇒ в первом ответ: 1) P.s. Ну можно проверить и остальные по желанию.
2. ~ - эквивалентность - значения равны.
→ - импликация - Ложь будет только в случае 1 → 0, во всех остальных -истинна.
Делаем всё тоже, что и в первой задаче.
1) (X~Z) /\ ( ¬X→Y)
1 0 1 0 : ( 1 ~ 1) /\ (0→0)
(1)/\(1) = 1 - Неверно, первая строка не совпала, дальше можно не проверять.
4) (Ну я каждое разбирать не буду, сразу к 4-му выражению перейду)
(X~Z) /\ ¬ (Y→Z)
1 0 1 0: (1 ~ 1)/\¬(0→1) : (1)/\¬(1) : 1/\0 = 0 -Первая строка совпала.
0 1 0 1: (0~0)/\¬(1→0) : (1)/\¬(0) : 1/\1 = 1 - Вторая строка совпала
1 1 1 0: (1~1)/\¬(1→1) : (1)/\¬(1) : 1/\0 = 0- Третья строка совпала
Значит ответ 4)