Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w
обозначают цепочки символов.
заменить (v, w)
нашлось (v)
Первая команда заменяет в строке первое слева вхождение цепочки v на
цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку.
Вторая команда проверяет, встречается ли цепочка v в строке исполнителя
Редактор. Если она встречается, то команда возвращает логическое значение
"истина", в противном случае возвращает значение "ложь".
Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (111)
заменить (111, 22)
заменить (2222, 1)
КОНЕЦ ПОКА
КОНЕЦ
Какая строка получится в результате применения приведённой программы к
строке вида 1…12…2 (63 единицы и 61 двойка)?
ОЧЕНЬ С ОЪЯСНЕНИЕМ
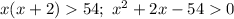
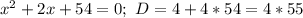
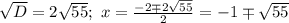
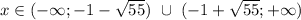
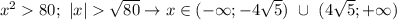
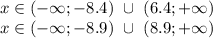
![F=a \to b = \overline a \lor b; \\ \overline F=\overline{\overline a \lor b}=a \land \overline b; \\ F=(x \in (-\infty;-8.4) \ \cup \ (6.4;+\infty)) \land \overline{x \in (-\infty;-8.9) \ \cup \ (8.9;+\infty)}= \\ (x \in (-\infty;-8.4) \ \cup \ (6.4;+\infty)) \land (x \in [-8.9;8.9])= \\ (x \in (-\infty;-8.4) \cap [-8.9;8.9]) \cup (x \in (6.4;+\infty) \cap [-8.9;8.9])= \\ (x \in [-8.9;-8.4)) \cup (x \in (6.4;8.9])=x \in [-8.9;-8.4) \cup (6.4;8.9];](/tpl/images/0296/0336/7d495.png)
![x \in false \cup [7;8] \to x=8](/tpl/images/0296/0336/46542.png)
Квадрат числа будет кратен четырем в том случае, если это число чётное, то есть ответом будет кол-во четных двузначных чисел, а это 45.
2. 3 бита это 2^3 = 1 из 8 вариантов. Значит четверки - это 1/8 от всех оценок, 64/8=8 четверок
3. Всего существует 5 четных цифр (включая 0). Из них можно составить 5^4 = 625 различных четырёхзначных комбинаций.