Скорее всего тебе необходимы алгоритмы для решения таких задач, они изображаются графически. Прикреплены два файла с этими алгоритмами.
Овалами обозначаются начало и конец алгоритмаТрапеция обозначаются ввод и вывод данныхПрямоугольниками обозначаются блоки где производятся расчетыДля первой задачи алгоритм прост:
Ввод длины стороны AВвод длины стороны BВвод длины стороны CРасчет длины медианы к стороне AРасчет длины медианы к стороне BРасчет длины медианы к стороне CВывод длины медианы к стороне AВывод длины медианы к стороне BВывод длины медианы к стороне CДля второй задачи:
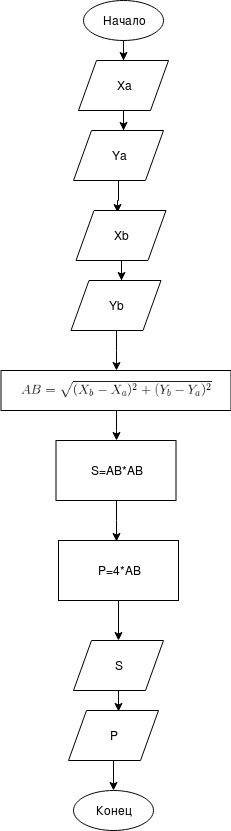
Ввод X координаты для первой точкиВвод Y координаты для первой точкиВвод X координаты для второй точкиВвод Y координаты для второй точкиРасчет по формуле расстояния между двумя точками - получаем сторону квадратаРасчет площади квадратаРасчет периметра квадратаВывод значения площади квадратаВывод значения периметра квадрата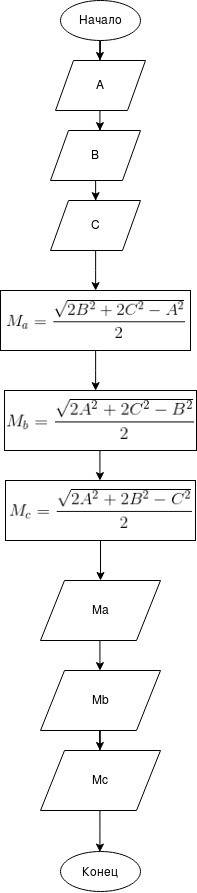
Можно решать через формулы для количества информации в сообщении, записанном алфавитом с известным количеством символов.
Здесь алфавит- это набор всех возможных значений показаний прибора (каждое из возможных показаний- один из символов алфавита). Значит, мощность алфавита равна:
Было сделано 50 измерений, и соответственно записано 50 значений показаний прибора. Каждая из этих записей- это один символ, записанный в сообщении. Значит, длина сообщения равна:
Далее, количество информации в одном символе (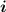 ) можно найти двумя путями:
) можно найти двумя путями:
1) Через формулу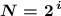 . Просто подбираем (по таблице степеней двойки или считая на калькуляторе) такое минимальное целое значение
. Просто подбираем (по таблице степеней двойки или считая на калькуляторе) такое минимальное целое значение 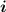 , чтобы два в этой степени дало значение не меньше чем
, чтобы два в этой степени дало значение не меньше чем 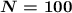 символов. Например:
символов. Например:
То есть, минимальная нужная нам степень равна 7. Значит, количество информации в одном символе (для нашего алфавита) равно:
2) Если вы уже проходили формулу расчёта через двоичный логарифм, то можно считать по ней. При этом, двоичный логарифм (которого может не быть в калькуляторе) можно заменить отношением десятичных либо натуральных логарифмов:
Раз получилось дробное значение, то выбираем следующее целое (большее, чем полученное по расчёту). То есть, число 7. Другими словами, округляем до целых, но не как обычно, а всегда в большую сторону. Опять же, мы получили, что:
Далее, считаем количество информации в сообщении (информационный размер сообщения):
Переводим в байты:
Это значение тоже можно было бы округлить до целых (всегда в большую сторону), ведь при хранении чаще всего хранят целое число байт. Но, в задаче не сказано про именно целое число байт, поэтому не будем округлять.
ответ: 43,75 байт