номер 9 Начнем считать количество путей с конца маршрута — с города К. Пусть NX — количество различных путей из города А в город X, N — общее число путей.
В К можно приехать из Е, В, Г или Ж, поэтому N = NК = NЕ + NВ + N Г + NЖ (*).
Аналогично:
NЕ = NБ + NВ = 1 + 1 = 2;
NЖ = NД = 1;
NВ = NА = 1;
NГ = NВ + NА + NД = 1 + 1 + 1 = 3;
NД = NА = 1;
NБ = NА = 1.
Подставим найденные значения в формулу (*): N = 2 + 1 + 3 + 1 = 7.
Источник: ГИА по информатике 31.05.2013. Основная волна. Центр, Урал. Вариант 1301.
Объяснение:
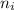вершин, то общее число рёбер будет суммой по всем компонентам связности: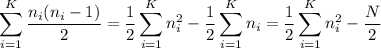
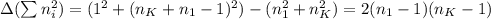
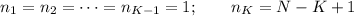
pro, sum:integer;
begin
write('Введите число: '); readln(n);
pro:=1; sum:=0;
while n>0 do
begin
pro:=pro*(n mod 10);
sum:=sum+(n mod 10);
n:=n div 10;
end;
writeln('Произведение = ', pro);
writeln('Сумма = ', sum);
end.