1. объясните, почему следующие предложения не являются высказывания ми 1) какого цвета этот дом? 2) число х не превосходит единицы. 3) 4x+ 3. 4) посмотрите в окно. 5) пейте томатный сок! 6) эта тема скучна. 7) рикки мартин самый популярный певец 8) вы были в театре?

👇

Ответ:

vladt12092002

07.10.2020

1) Содержит вопрос, а не утверждение.
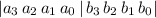
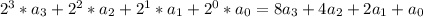
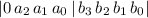
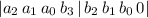
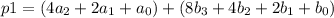
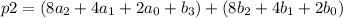
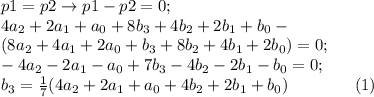
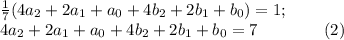
2) на самом деле это ВЫСКАЗЫВАНИЕ, оно несет информацию.
3) Непонятен смысл и назначение этого выражения.
4) Не несет информации (например, о том, зачем это делать)
5) Не несет информацию о том, зачем это делать
6) Не несет конкретной информации о теме.
7) Не несет информации о том, среди кого.
8) Это вопрос, а не утверждение.

4,8(61 оценок)

Открыть все ответы

Ответ:

мария21112006

07.10.2020

В приложении дана блок-схема с алгоритмом, вычисляющим значение функции F по рекуррентной схеме.
Ниже приводится запись программы на языке Pascal, содержащая две функции - рекуррентную F (строго в соответствии с алгоритмом) и рекурсивную Fr.
Вывод иллюстрирует работу программы для значения аргумента n=6

function F(n: integer): integer;
{рекуррентная}
var
i, p: integer;
fn1, fn2: integer;

begin
case n of
    1: Result := 1;
    2: Result := 2;
else
    begin
      fn2 := 1;
      fn1 := 2;
      for i := 3 to n do
      begin
        p := 2 * fn1 + (i - 2) * fn2;
        fn2 := fn1;
        fn1 := p
      end;
      Result := p
    end
end
end;

function Fr(n: integer): integer;
{рекурсивная - оцените изящество рекурсии!}
begin
case n of
    1: Result := 1;
    2: Result := 2;
else Result := 2 * Fr(n - 1) + (n - 2) * Fr(n - 2)
end
end;

begin
writeln(F(6), ' ', Fr(6))
end.

Тестовое решение:
142 142

ответ: значение функции F(6) равно 142.

4,4(38 оценок)

Ответ:

Killjoy008

07.10.2020

Задача достаточно интересная, получил удовольствие от решения.
Шестнадцатиричное число, занимающее два разряда, может рассматриваться как две тетрады двоичных чисел. Пронумеруем разряды слева направо, тогда можно представить двухзначное 16-ричное число следующим набором битов:
$|a_3\,a_2\,a_1\,a_0\,|\,b_3\,b_2\,b_1\,b_0|$
Индексы, кроме положения бита, показывают степень двойки, на которую надо умножить бит, чтобы перейти к десятичному эквиваленту шестнадцатиричной цифры, т.е. старшая цифра в десятичной системе запишется как
2^3*a_3+2^2*a_2+2^1*a_1+2^0*a_0=8a_3+4a_2+2a_1+a_0

2^3*a_3+2^2*a_2+2^1*a_1+2^0*a_0=8a_3+4a_2+2a_1+a_0

Умножение числа на 2 в двоичной системе эквивалентно его сдвигу влево на один разряд. При этом старший разряд старшей тетрады должен перейти в новую, третью тетраду или он будет утерян. Но по условию, после умножения число по-прежнему имеет два разряда, следовательно мы должны потерять старший разряд безболезненно, а это возможно только если он нулевой.
Тогда первоначальное число должно быть записано как
$|0\,a_2\,a_1\,a_0\,|\,b_3\,b_2\,b_1\,b_0|$
а после удвоения его запись примет вид
$|a_2\,a_1\,a_0\,b_3\,|\,b_2\,b_1\,b_0\,0|$
Запишем сумму цифр исходного числа p1:
p1=(4a_2+2a_1+a_0)+(8b_3+4b_2+2b_1+b_0)

Теперь запишем сумму удвоенного числа p2:
p2=(8a_2+4a_1+2a_0+b_3)+(8b_2+4b_1+2b_0)

По условию эти две суммы равны и мы составляем уравнение:
$p1=p2 \to p1-p2=0; \\ 4a_2+2a_1+a_0+8b_3+4b_2+2b_1+b_0- \\ (8a_2+4a_1+2a_0+b_3+8b_2+4b_1+2b_0)=0; \\ -4a_2-2a_1-a_0+7b_3-4b_2-2b_1-b_0=0; \\ b_3= \frac{1}{7}(4a_2+2a_1+a_0+4b_2+2b_1+b_0)\qquad \qquad (1)$
Полученное уравнение решается на множестве двоичных чисел.
Поскольку исходное число двузначное, по крайней мере в старшем разряде оно содержит цифру, отличную от нуля. Следовательно, b3 не может равняться нулю и остается только положить b3=1. Тогда уравнение (1) примет следующий вид:
$\frac{1}{7}(4a_2+2a_1+a_0+4b_2+2b_1+b_0)=1; \\ 4a_2+2a_1+a_0+4b_2+2b_1+b_0=7 \qquad \qquad (2)$
Учитывая, что каждый бит может принимать значения только 0 и 1, мы должны найти такие комбинации бит, которые дадут в сумме 7=4+2+1, потому что у нас в уравнении только такие коэффициенты. Сгруппируем члены в (2):
$4(a_2+b_2)+2(a_1+b_1)+(a_0+b_0)=7 \to \begin {cases} a_2+b_2=1 \\a_1+b_1=1 \\a_0+b_0=1 \end {cases} \qquad (3)$
Полученная система уравнений будет иметь 7 вариантов решений (вариант a2=a1=a0=0 исключается в силу необходимости наличия цифры в старшем разряде), которым в старшем разряде будут соответствовать цифры от 001(2) до 111(2) или от 1(10) до 7(10).

ответ: 7

Замечание: Из (3) можно легко найти числа, которые соответствуют заданным условиям: 30, 45, 60, 75, 90, 105, 120 (все в десятичной системе счисления). В 16-ричной системе они запишутся как 1E, 2D, 3C, 4B, 5A, 69, 78.

4,8(57 оценок)

Это интересно:

Образование

06.01.2021

Клюква стоит 250 рублей за кг, а малина 200....

Образование

16.03.2023

Решить систему уравнений x2 + y2 + xy = 3...

Образование

05.08.2020

Решить систему уравнений x2 + xy +y2 = 13...

Образование