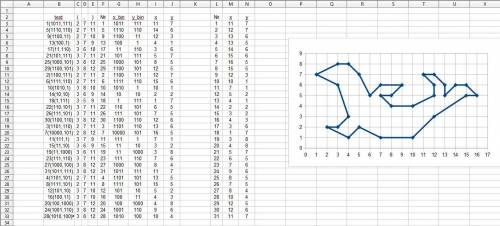
Координаты даны в двоичной системе счисления, поэтому переводим их в десятичную.
Потом сортируем по порядку по номерам точек.
И отмечаем точки на графике, соединяя соседние отрезком.
Я все эти преобразования сделал в таблице Эксель.
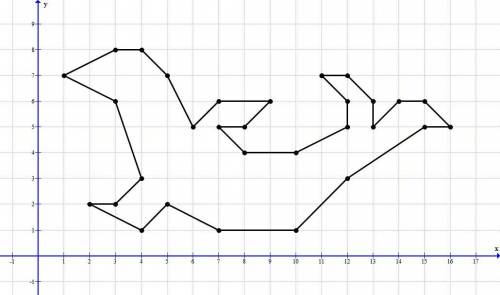
Саму таблицу и картинку, полученную после нанесения всех точек смотри внизу.
А вот координаты точек, отсортированные и в десятичной системе:
№ x y
1 11 7
2 12 7
3 13 6
4 13 5
5 14 6
6 15 6
7 16 5
8 15 5
9 12 3
10 10 1
11 7 1
12 5 2
13 4 1
14 2 2
15 3 2
16 4 3
17 3 6
18 1 7
19 3 8
20 4 8
21 5 7
22 6 5
23 7 6
24 9 6
25 8 5
26 7 5
27 8 4
28 10 4
29 12 5
30 12 6
31 11 7
def check_perfect(number:int, dividers = []):
for i in range(1, number):
if number%i == 0:
dividers.append(i)
if sum(dividers) == number:
return 1
def get_div(num, div = []):
for i in range(1, num):
if num%i == 0:
div.append(i)
return div
def main():
number = int(input())
if check_perfect(number):
print(' '.join(str(num) for num in get_div(number)))
else:
print(0)
if __name__ == '__main__':
main()
Объяснение:
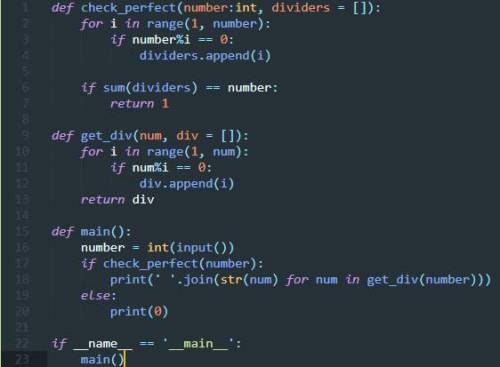
На случай, если сайт сломает табуляции в коде (А он их сломает), ниже представлен скриншот оригинала кода. Программа протестирована.
Напишу веса разрядов начиная от первого справа от запятой, и далее, по порядку:
Двоичная система: 2^(-1)=1/2, 2^(-2)=1/4, 2^(-3)=1/8, 2^(-4)=1/16 ... итд
Восьмеричная: 8^(-1)=1/8, 8^(-2)=1/64, 8^(-3)=1/512 ... итд
Шестнадцатеричная: 16^(-1)=1/16, 16^(-2)=1/256, 16^(-3)=1/4096 ... итд
Вес разрядов слева от точки равен основанию системы в степени 0, 1, 2, 3 ... итд (то есть 2^(n-1), где n- номер разряда считая от первого слева от запятой).
Напишу веса разрядов начиная от первого слева от запятой, и далее, по порядку:
Двоичная система: 2^0=1, 2^1=2, 2^2=4, 2^3=8 ... итд
Восьмеричная: 8^0=1, 8^1=8, 8^2=64 ... итд
Шестнадцатеричная: 16^0=1, 16^1=16, 16^2=256 ... итд