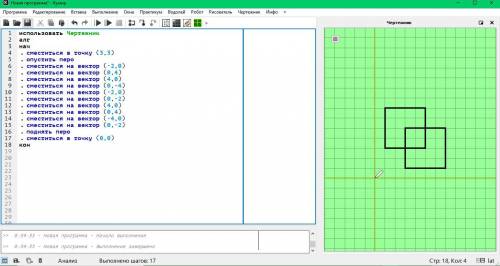
1. Квадраты
использовать Чертежник
алг
нач
сместиться в точку (3,3)
опустить перо
сместиться на вектор (-2,0)
сместиться на вектор (0,4)
сместиться на вектор (4,0)
сместиться на вектор (0,-4)
сместиться на вектор (-2,0)
сместиться на вектор (0,-2)
сместиться на вектор (4,0)
сместиться на вектор (0,4)
сместиться на вектор (-4,0)
сместиться на вектор (0,-2)
поднять перо
сместиться в точку (0,0)
кон
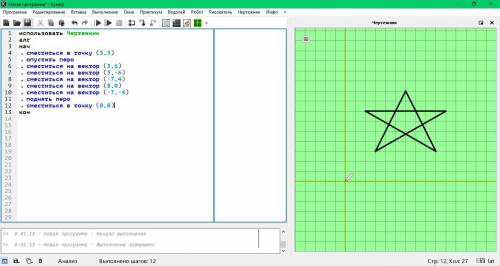
2. Звезда
использовать Чертежник
алг
нач
сместиться в точку (3,3)
опустить перо
сместиться на вектор (3,6)
сместиться на вектор (3,-6)
сместиться на вектор (-7,4)
сместиться на вектор (8,0)
сместиться на вектор (-7,-4)
поднять перо
сместиться в точку (0,0)
кон
Объяснение:
картинки
Утверждение: если всё вышеперечисленное не выполнено, можно просто много раз делить на максимальное из чисел; на последнем шаге, возможно, надо будет вычесть максимальное, а не разделить на него. При этом будет получен 0 за минимальное число шагов. Это можно показать и строго, но "на пальцах" это верно, так как деление на максимальное из чисел - операция, с которой число уменьшается быстрее всего.
Код (Python 3):
N = int(input())
_ = int(input())
A = list(map(int, input().split()))
if N == 0:
print(0)
elif 0 in A:
print(1)
elif all(elem == 1 for elem in A):
print(N)
else:
M = max(A)
count = 0
while N != 0:
if N != M:
N //= M
else:
N -= M
count += 1
print(count)
var a:array[1..9] of longint;
i,n:longint;
begin
readln(n);
for i:=0 to 9 do a[i]:=0;
while n>=1 do
begin
a[n mod 10]:=a[n mod 10]+1;
n:=floor(n/10);
end;
for i:=0 to 9 do
if a[i]>2 then writeln(i);
end.