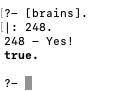
Так как язык не указан, приведу пример на SWI-Prolog.
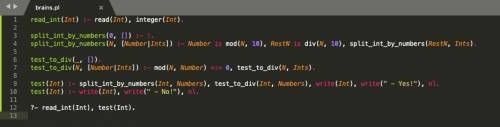
Код:
read_int(Int) :- read(Int), integer(Int).split_int_by_numbers(0, []) :- !.split_int_by_numbers(N, [Number|Ints]) :- Number is mod(N, 10), RestN is div(N, 10), split_int_by_numbers(RestN, Ints).test_to_div(_, []).test_to_div(N, [Number|Ints]) :- mod(N, Number) =:= 0, test_to_div(N, Ints). test(Int) :- split_int_by_numbers(Int, Numbers), test_to_div(Int, Numbers), write(Int), write(" - Yes!"), nl.test(Int) :- write(Int), write(" - No!"), nl.?- read_int(Int), test(Int).
var
a,b,t,N:integer;
function F(x:integer):integer;
begin
F:=16*(6-x)*(6-x)-450;
end;
begin
a:=-20; b:=20;
N:=0;
for t:=-20 to 20 do
if (F(t)>=0) then N:=N+1;
Write(N)
end.
Переменные a и b получают начальные значения, но дальше не используются, поэтому их рассматривать не нужно.
Все переменные в программе объявлены целочисленными, поэтому анализируем алгоритм также в целых числах.
Переменная t последовательно принимает значения от -20 до 20, следовательно, можно записать, что t ∈ [-20;20]
Для каждого t вычисляется значение некоторой функции F(t) и подсчитывается N - количество случаев, когда значение F(t) неотрицательно. Найденное N затем выводится. Ставится задача определить значение N.
Проанализируем функцию F(t). После простого преобразования получаем
F(t)=16(6-t)²-450
Теперь надо найти решение неравенства F(t)≥0.
Поскольку решение выполнятся в целых числах, то значение в правой части неравенства достаточно записать с точностью один знак после запятой.
На интервале [-20;20] первому условию удовлетворит 21 точка, второму условию удовлетворят 9 точек. Всего получится 21+9=30 точек.
ответ: Будет выведено число 30