a:array[0..9] of integer;
i,y,min:integer;
begin
randomize();
for i:=0 to 9 do
begin
y:= random(10);
a[i]:= y;
end;
for i:=0 to 9 do write(a[i],' ');
writeln(' - десять випадковых чисел');
min:=a[0];
for i:=1 to 9 do
if a[i]<min then min:=a[i];
writeln(min, ' - минимальне число.');
end.
ответ: 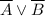 .
.
Пошаговое объяснение:
Во-первых, как можно заметить, от C значение функции не зависит.
Особенно это хорошо видно на последних двух строчках. Если убрать переменную C, то получиться таблица из 4 строк:
A B F
0 0 1
0 1 1
1 0 1
1 1 0
Это таблица истинности для отрицания И: 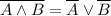 - ответ.
- ответ.
На этом можно было бы остановиться (проверить по таблице истинности с учётом бесполезного С), но сделаем ещё кое-что - выведем это шаг за шагом, докажем, что С - бесполезная и никому не нужная переменная.
Запишем то же выражение в совершенной конъюнктивной нормальной форме. Выберем стоки, которые обращают выражение в Ложь.
A B C F
1 1 0 0
1 1 1 0
Две строки - две скобки. Единица в таблице означает отрицание переменной в скобке. Получаем 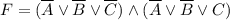 .
.
Тут уже видно, что переменная С на результат не влияет. Упростим и приведём это к выражению выше.
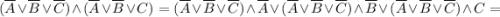
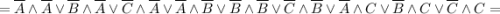
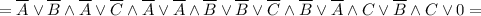
![= \overline A \lor \overline B \lor [(\overline B \land \overline A) \lor (\overline A \land \overline B)] \lor [(\overline C \land \overline A) \lor(\overline A \land C)] \lor [(\overline C \land \overline B) \lor (\overline B \land C)] =](/tpl/images/1360/3469/09f19.png)
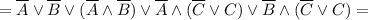
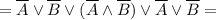
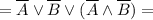
![= [(\overline A \lor \overline A) \land (\overline A \lor \overline B)] \lor \overline B =](/tpl/images/1360/3469/ce0d8.png)
![= [\overline A \land (\overline A \lor \overline B)] \lor \overline B =](/tpl/images/1360/3469/cc585.png)
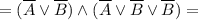
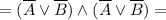
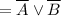 - ответ.
- ответ.
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 0
1 1 0 0
1 1 1 1
Сделаем простое преобразование:
Мы получили конъюнкцию b и выражения в круглых скобках. Она ложна, если ложно хотя бы b в этом выражении. Поищем колонку, в которой всегда стоит ноль, если ноль в колонке F. Это предпоследняя колонка, следовательно она содержит значения для b (ведь в колонке указано значение одной переменной)
? ? b F
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 0
1 1 0 0
1 1 1 1
А теперь воспользуемся истинным значением F. F истинно только если истинны одновременно и b, и выражение в скобках. А в скобках находится дизъюнкция с и инверсии a. Дизъюнкция ложна, если ложны оба её компонента, т.е. если ложно с и истинно а (из-за инверсии). Это дает нам комбинацию cabF=0110 или acbF=1010. Находим одну из этих строк: 1010 третья снизу. Следовательно, подписи колонок acbF.
a c b F
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 0
1 1 0 0
1 1 1 1