Появилось две линии, стрелочка начала зацикливаться. Получается алгоритм будет выполняться бесконечное количество раз. Чтобы более точно ответить на письменный вопрос - можете провести идентичные действия:
Заходим в ГРИС.
Нажимаем "Начать"
Нажимаем F4(поворот) три раза. (В условии сказано, что исходное положение: ГРИС — в левом верхнем углу, направление — вниз.)
Теперь нажимаем F8(цикл) - выбираем: Пока впереди не стена.
Следующим этапом нажимаем F5 (описание). В появившейся строке нужно написать ПУТЬ и нажать Enter. Чтобы отключить окно нажимаем Esc. Жмем ещё два раза Enter.
Нажимаем: F4 - F3 - F4 (поворот - прыжок - поворот).
При откладки (вверху) спускаемся в самый низ на панели наших действий (слева).
Жмем F8 - Пока впереди стена.
Жмем F2 (шаг).
Жмем на откладку вверху и смотрим результат
Готово))
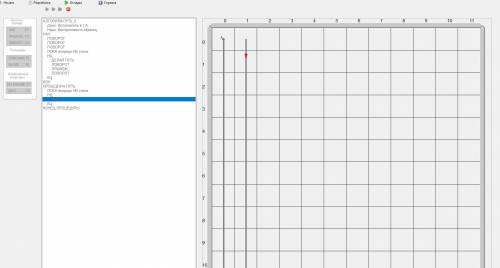
Появилось две линии, стрелочка начала зацикливаться. Получается алгоритм будет выполняться бесконечное количество раз. Чтобы более точно ответить на письменный вопрос - можете провести идентичные действия:
Заходим в ГРИС.
Нажимаем "Начать"
Нажимаем F4(поворот) три раза. (В условии сказано, что исходное положение: ГРИС — в левом верхнем углу, направление — вниз.)
Теперь нажимаем F8(цикл) - выбираем: Пока впереди не стена.
Следующим этапом нажимаем F5 (описание). В появившейся строке нужно написать ПУТЬ и нажать Enter. Чтобы отключить окно нажимаем Esc. Жмем ещё два раза Enter.
Нажимаем: F4 - F3 - F4 (поворот - прыжок - поворот).
При откладки (вверху) спускаемся в самый низ на панели наших действий (слева).
Жмем F8 - Пока впереди стена.
Жмем F2 (шаг).
Жмем на откладку вверху и смотрим результат
Готово))

Перебор:
159, 519, 591, 195, 915, 951. =>6.
Комбинаторика. Переопределим задачу так: сколько существует перестановок 3х предметов, или сколькими можно расставить три цифры на свои места. ответ 3!=3*2*1=6.
Можно получить из таких суждений:
На первое место можно выбрать одну из 3х цифр. Всего возможных вариантов выбрать одну из 3х цифр три.
На второе место можно выбрать уже одну из 2х цифр, т.к. одна уже была поставлена на первое место. Вариантов 2. На последнее место останется какая-то одна цифра. Вариантов 1. Отсюда всех возможных вариантов:
3*2*1