ответ: Python
nk = input().split()
N = int(nk[0])
K = int(nk[1])
count = 0
prev = set('a')
for x in range(N):
s = input().split()
set_s = set(s[1:])
if set_s.issuperset(prev) == False:
count += 1
prev = set_s
print(count)
Объяснение:
Решал, подразумевая, что одно и то же K не может повторяться несколько раз на одной строке.
Псевдокод алгоритма:
1. Получаем N
2. Получаем K
3. Создаем переменную count для подсчета операций
4. Создаем множество prev для сохранения каждого предыдущего множества
5. Прогоняем цикл N раз:
6. Получаем список s от пользователя
7. Получаем множество set_s из списка s
8. Проверяем, если предыдущее множество prev не является подмножеством set_s:
9. То к count прибавляем 1
10. Присваиваем prev значение set_s
Тут надо вручную составить таблицу истинности для этого лог.выражения (можно назвать его функцией F).
Её начало уже записано в задании - это три столбца с входными сигналами (A, B, C).
После этого делаете и заполняете столбцы с инверсными входными сигналами (если такие используются в выражении) - тут это будут ¬A, ¬C.
Затем, выполняете по порядку лог. операции из этого выражения (и результаты для каждой заносите в свой столбец. Последний из этих столбцов будет содержать результаты последней лог. операции - они же и есть результаты для всей функции F.
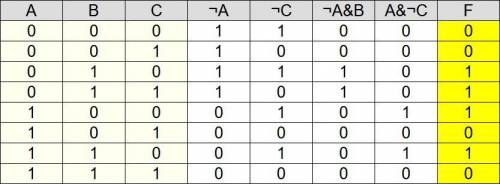
Вся таблица истинности показана на скрине внизу, а значения для функции F (которые нужно занести в ответ) там выделены жёлтым цветом. Здесь я их выпишу отдельно:
F
0
0
1
1
1
0
1
0
Можно конечно обойтись и без заполнения таблицы - а сразу, подставляя в лог. выражение текущие значения входных сигналов, в уме просчитывать что будет на выходе, и записывать эти значения сразу в ответ. Но, так делать посложнее, поэтому всё же таблицу лучше заполнить, там каждый шаг расписывается.
begin
write('a = '); readln(a);
write('b = '); readln(b);
write('c = '); readln(c);
write('d = '); readln(d);
if a<b then min1:=a else min1:=b;
if c<d then min2:=c else min2:=d;
if min1>min2 then max:=min1 else max:=min2;
writeln('max = ',max);
end.
Пример:
a = 5
b = 2
c = 1
d = 4
max = 2