1)#include <iostream>
using namespace std;
int main() {
int a=1,b=1,c=0,d=1;
int otvet=a*(-1)+b^c-d;
cout<<otvet;
}
2)#include <iostream>
using namespace std;
int main() {
int a = 1, b = 1, c = 1, d = 1;
int otvet=a*(-1)+b^c-d;
cout<<otvet;
}
3)#include <iostream>
using namespace std;
int main() {
int a = 0, b = 0, c = 0, d = 0;
int otvet=a*(-1)+b^c-d;
cout<<otvet;
}
4)#include <iostream>
using namespace std;
int main() {
int a = 0, b = 1, c = 1, d = 0;
int otvet=-(a+b^c+(-b))+a^d;
cout<<otvet;
}
5)#include <iostream>
using namespace std;
int main() {
int a = 1, b = 0, c = 0, d = 1;
int otvet=-(a+b^c+(-b))+a^d;
cout<<otvet;
}
6)#include <iostream>
using namespace std;
int main() {
int a = 1, b = 1, c = 1, d = 1;
int otvet=-(a+b^c+(-b))+a^d;
cout<<otvet;
}
7)#include <iostream>
using namespace std;
int main() {
int a = 0, b = 0, c = 0, d = 0;
int otvet=-(a+b^c+(-b))+a^d;
cout<<otvet;
}
Объяснение:
Код неверный
Объяснение:
Вот код:
Первый (простой, работает медленнее)
#include<iostream>
using namespace std;
int main() {
int n;
cin >> n;
for(int i = 1; i <= n; i++) {
if(sqrt(i) == (int)sqrt(i))
cout << i << ' ';
}
}
Фактически мы просто для каждого числа проверяем, является ли его квадратный корень целым числом.
#include<iostream>
using namespace std;
int main() {
int n;
cin >> n;
int x = 1, d = 3;
while(x <= n) {
cout << x << ' ';
x += d;
d += 2;
}
}
Решение основывается на этом утверждении:
Разница между квадратами двух последовательных натуральных чисел больше на 2 разницы между предыдущими двумя квадратами, например:
4 - 1 + 2 = 9 - 4
Доказательство:
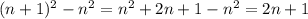
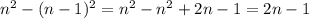
Из чего получаем:
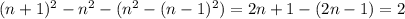
Доказано.
Поэтому я проголосовал бы за ответ -1.