ответ: 1. 256
2. 262144²
3. 4398,0465 Гбит
4. 125 000 байт
5. 250 Мбит
Объяснение: 1. 2^21=2097152 бит,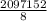 
=262144 байт, 
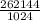=256;
2. там идет много раз перемножение с гигобайт в мегабайт в килобайт в байт и в бит а после находится корень из этого числа: √(68 719 476 736)
3. 1 гигабит = 10^9бит = 1 000 000 000 (миллиард) бит.
2^39=549 755 813 888 байт, а поэтому умножим на 8 и получим биты:
4 398 046 511 104 бит, и поделим на миллиард, получится 4398,0465 Гбит
4. Мегаби́т — количество информации, 10^6 или 1 000 000 (миллион) бит.
если у нас есть 1 000 000 бит то найдем сколько это байт поделив на 8:
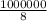=125 000 байт.
5. найдём сколько бит в 0,25 Гбит: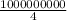 
=250 000 000 бит,
зная что в одном Мегабите 1 миллион бит, поделим и получим 250 штук(Мбит в 1/4 Гбит)
Нормализованной (экспоненциальной) называется запись отличного от нуля вещественного числа в виде m * Pq, где q – целое число (положительное, отрицательное или ноль) , а m – правильная P-ичная дробь, у которой первая цифра после запятой не равна 0, то есть 1 / P ≤ m < 1. При этом m называется мантиссой числа, а q – порядком числа.
Нормализация мантиссы позволяет сэкономить один разряд в ее двоичном представлении. В обоих случаях заранее известно, что первый значащий разряд равен единице, поэтому его можно не хранить. Иногда это называется использованием неявного старшего бита.
Нормализация мантиссы результата независимо от режима не выполняется.
Нормализация мантиссы результата заключается в повторении операции сдвига мантиссы на один десятичный разряд с обнулением младшего разряда, а также в уменьшении порядка на единицу до тех пор, пока в знаковом разряде К2 ( Д9) не будет находиться наибольшая значащая цифра мантиссы. При переполнении разрядной сетки в области мантиссы выполнение этой процедуры может привести к переполнению разрядной сетки в области порядка.
00111001000100100000000000000000 - нули слева убираем:111001000100100000000000000000 - нормализуем мантиссу:
1.11001000100100000000000000000 х 2^29.
Теперь мантисса нормализована.