2
Объяснение:
Алгорим тут, мягко говоря, странноват.
t :=a[i];
a[i-1] := a[0];
a[0] := t
Никакого t здесь не нужно, достаточно написать
a[i-1] := a[0];
a[0] := a[i]
В цикле, начиная с третьего по порядку элемента, производится его сравнение с самым первым элементом (вначале его значение равно 5).
Присваивание a[i-1] := a[0] в теле цикла никак на a[0] не влияет и на сравнение не влияет, поэтому забудем о нем.
Таким образом, существенным оказывается лишь факт попадания на место a[0] элемента, меньшего a[0] и каждое такое попадание увеличивает счетчик с на 1. Первонаяальное значение с нулевое, так что с отражает количество попаданий в a[0] элементов, меньших его значения. Анализ значений элементов с a[2] по a[9] показывает, что сначала в a[0] попадает 2 (2 < 5), а затем 0 ( 0 < 2). Поэтому с = 2.
32
Пояснение:
дополнительно смотреть изображение
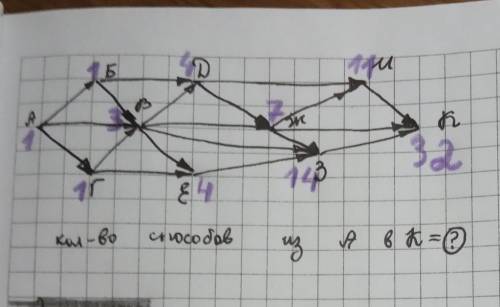
Отмечу,что в этой задаче мы имеем дело с ориентированным графом (графом, у которого ребра имеют направление). Т.е. ребра имеют вид стрелок. Две вершины, соединенные напрямую стрелкой, называются смежными. Вершина, из которой выходит стрелка, называется предком, а вершина, в которую входит стрелка – потомком.
Несложно понять, что количество путей, которыми можно попасть в некоторую вершину, равно сумме количеств путей предков этой вершины.
Каждой вершине, начиная с начальной (A), поставим в соответствие индекс, равный количеству путей, которыми можно попасть в эту вершину. Для вершины A (начало пути) индекс всегда равен 1 (в начало пути можно попасть единственным образом – никуда не двигаясь). Теперь сформулируем правило: индекс вершины равен сумме индексов его предков.
тогда для вершины Б=А=1
Г=А=1
В=А+Б+Г=1+1+1=3
Д=Б+В=1+3=4
Е=В+Г=3+1=4
Ж=В+Д=3+4=7
З=Е+В+Ж=4+3+7=14
И=Ж+Д=7+4=11
К=И+Ж+З=11+7+14=32
Очевидно, что мы могли посчитать индекс только тех вершин, индексы предков которых уже посчитаны. Двигаясь последовательно, мы рассчитали индексы всех вершин.
Индекс вершины К и будет ответом задачи.
алг
нач
влево
нц пока снизу свободно
периметр
мост
кц
кон
алг мост
нач
вниз
влево
нц пока снизу не свободно
если слева свободно
то
влево
все
кц
кон
алг периметр
нач
закрасить
вправо
нц пока снизу не свободно
закрасить
вправо
кц
закрасить
вниз
нц пока слева не свободно и снизу свободно
закрасить
вниз
кц
закрасить
влево
нц пока сверху свободно
закрасить
вверх
кц
нц пока сверху не свободно
закрасить
влево
кц
закрасить
вверх
закрасить
вправо
нц пока снизу не свободно
вправо
кц
вниз
нц пока слева не свободно
вниз
кц
кон