а) язык программирования
Объяснение:
К инструментальному программному обеспечению относят: системы программирования – для разработки новых программ, например, Паскаль, Бейсик. Обычно они включают: редактор текстов, обеспечивающий создание и редактирование программ на исходном языке программирования (исходных программ), транслятор, а также библиотеки подпрограмм; инструментальные среды для разработки приложений, например, C++, Delphi, Visual Basic, Java, которые включают средства визуального программирования; системы моделирования, например, система имитационного моделирования MatLab, системы моделирования бизнес-процессов BpWin и баз данных ErWin и другие.
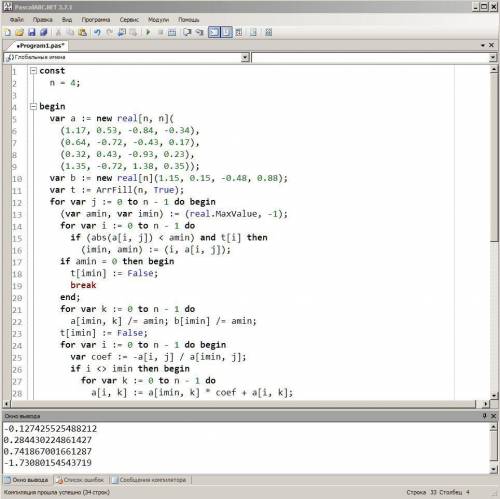
const
n = 4;
begin
var a := new real[n, n](
(1.17, 0.53, -0.84, -0.34),
(0.64, -0.72, -0.43, 0.17),
(0.32, 0.43, -0.93, 0.23),
(1.35, -0.72, 1.38, 0.35));
var b := new real[n](1.15, 0.15, -0.48, 0.88);
var t := ArrFill(n, True);
for var j := 0 to n - 1 do begin
(var amin, var imin) := (real.MaxValue, -1);
for var i := 0 to n - 1 do
if (abs(a[i, j]) < amin) and t[i] then
(imin, amin) := (i, a[i, j]);
if amin = 0 then begin
t[imin] := False;
break
end;
for var k := 0 to n - 1 do
a[imin, k] /= amin; b[imin] /= amin;
t[imin] := False;
for var i := 0 to n - 1 do begin
var coef := -a[i, j] / a[imin, j];
if i <> imin then begin
for var k := 0 to n - 1 do
a[i, k] := a[imin, k] * coef + a[i, k];
b[i] := b[imin] * coef + b[i]
end
end
end;
b.PrintLines
end.
/
Объяснение:
А) Обычно используется для статистической обработки результатов эксперимента, когда по заданному набору точек на плоскости (хотя можно и не только для плоскости применять) получают функцию в виде уравнения (т. е. аналитически заданную), непрерывную в области, заданной этими точками, которая максимально близко соответствует этому заданному набору точек. Такое определение функции обычно называется табличным, а полученную в результате в аналитическом виде функцию — линией регрессии. Критерий её поиска — минимизация суммы квадратов отклонений данной функции (линии регрессии) от изначально заданных точек, поэтому и называется «метод наименьших квадратов».
Б) основная тенденция изменения чего-либо: например, в математике — временного ряда.
В) Линия проходит через центр тяжести выборочных данных,
то есть выполняется равенство:
y=b1+sum(bi·xi)
Г) Нет, не может. Потому что в этом случае параллельно опустив тренд до первой же точки , мы уже добьемся лучшего совпадения с экспериментальными данными. Все расстояния от тренда до экспериментальных точек уменьшатся, а, значит, уменьшится и сумма квадратов расстояний.
источник:https://murnik.ru/dlja-chego-ispolzuetsja-metod-naimenshih-kvadratov-chto-takoe-trend-kak-raspolagaetsja-linija-trenda-postroennaja-po-mnk-otnositelno-jeksperimentalnyh-tochek-mozhet-li-trend-postroennyj-po-mnk-projti