begin
var count := 0;
var a := Range(ReadInteger('a='), ReadInteger('b='))
.Select(t -> t.ToString.JoinIntoString(' ').ToIntegers)
.Where(t -> t.Count.IsEven);
foreach var x in a do
begin
var (b, i) := (true, 0);
while (b) and (i < x.Length - 1) do
begin
if (x[i].IsOdd and x[i + 1].IsOdd) or (x[i].IsEven and x[i + 1].IsEven)
then b := false;
inc(i, 2);
end;
if (i = x.Length) and (b) then inc(count);
end;
count.Println;
end.
==============================
AKS-Test.
==============================
Обычно, когда проводят тест на простоту сталкиваются с тем, что определить простоту числа в большинстве тестов можно лишь с некоторой вероятностью.
Но математика не стоит на месте и сравнительно недавно появился AKS-тест, позволяющий быстро и гарантированно определить, является ли число простым.
Суть метода такова. Пусть число, которое мы тестируем обозначается A. У нас есть такое выражение: 
. Если раскрыть скобки и привести это дело к многочлену вида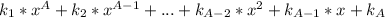 
и все коофиценты k в этом многочлене делятся на A без остатка, то число А - простое. Без вариантов.
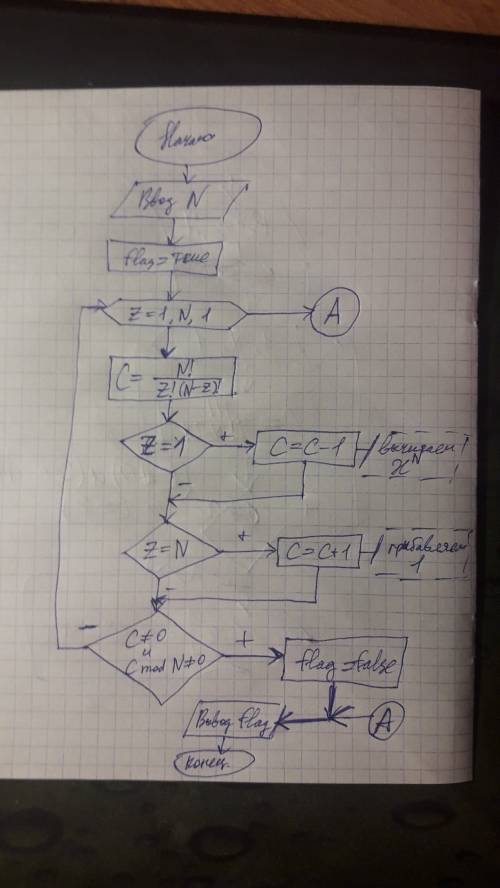
Блок-схема с числом n представлена на рисунке 1.
В цикле: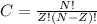 
. (! - факториал)
P.S. В блок-схеме есть элемент вида (А). Он использовался для связи, так как места на стрелку справа не оказалось. Можешь их убрать и соединить освободившиеся места стрелкой.
При выполнении оператора вывода write (14, 15, 16) отобразиться 141516