#include <iostream>
#include <vector>
using namespace std;
bool isLeap(int y){
return (y % 400 == 0 || (y % 4 == 0 && y % 100 != 0));
}
signed main(){
string s, cur;
cin >> s;
vector<int> d;
for(int i = 0; i < s.length(); i++){
if(s[i] == '.'){
d.push_back(stoi(cur));
cur.clear();
}
else
cur += s[i];
}
d.push_back(stoi(cur));
int k = d[0];
d[1]--;
while(d[1] > 0){
if(d[1] == 2) k += 28 + isLeap(d[2]);
else if((d[1] < 8 && d[1] % 2 == 1) || (d[1] >= 8 && d[1] % 2 == 0)) k += 31;
else k += 30;
d[1]--;
}
cout << (365 + isLeap(d[2])) - k + 1;
}
Для определенности назову сами символы как-нибудь:
A (0.084), B (0.168), C (0.336), D (0.0336), E (0.3784)
Алгоритм Хаффмана:
- упорядочиваем символы по возрастанию
- сливаем вместе два символа с наименьшими вероятностями, получаем составной символ с вероятностью, равной сумме вероятностей
- повторяем, пока не останется один символ
По сути это строит дерево Хаффмана, но мне рисовать весь процесс не хочется, буду писать в строчку:
D (0.0336), A (0.084), B (0.168), C (0.336), E (0.3784) - сливаем D и A, получается (D, A) с вероятностью 0.0336 + 0.084 = 0.1176
(D, A) (0.1176), B (0.168), C (0.336), E (0.3784) - сливаем (D, A) и B, получается ((D, A), B) с вероятностью 0.1176 + 0.168 = 0.2856
((D, A), B) (0.2856), C (0.336), E (0.3784) - сливаем ((D, A), B) и C, получается (((D, A), B), C) с вероятностью 0.2856 + 0.336 = 0.6216
E (0.3784), (((D, A), B), C) (0.6216) - сливаем в (E, (((D, A), B), C)), для проверки: вероятность 0.3784 + 0.6216 = 1
(E, (((D, A), B), C)) (1)
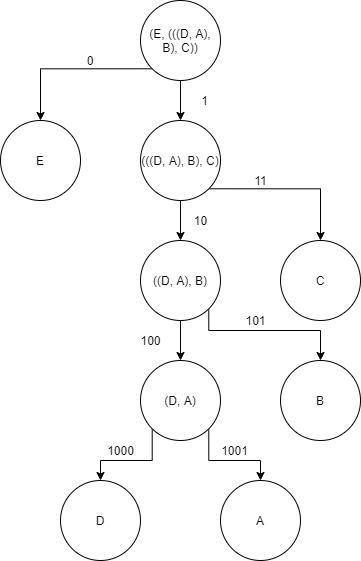
Готово! Если хочется перерисовать в виде бинарного дерева, у родителя (x, y) потомки x и у, мой вариант (для компактности он изображен немного искаженно) во вложении.
Осталось получить коды символов. Корню присваиваем пустой код, для левого потомка приписываем к коду родителя 0, для правого 1.
Получаем коды: A = 1001, B = 101, C = 11, D = 1000, E = 0.
Эффективность кодирования - это ожидаемая длина кода. Она в данном случае равна
0,084 * 4 + 0,168 * 3 + 0,336 * 2 + 0,0336 * 4 + 0,3784 * 1 = 2,0248 бит
Для сравнения, по формуле Шеннона количество информации в битах на один символ
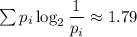
N=2^I
N=64
64=2^I
64=2^6
6 бит
6 бит*20 символов=120 бит
1 байт=8 бит
120:8=15 байт
пс. нуб в информатике