Объяснение:
В цифровой схемотехнике цифровой сигнал - это сигнал, который может принимать два значения, рассматриваемые как логическая "1" и логический "0".
Логические схемы могут содержать до 100 миллионов входов и такие гигантские схемы существуют. Представьте себе, что булева функция (уравнение) такой схемы была потеряна. Как восстановить её с наименьшими потерями времени и без ошибок? Наиболее продуктивный разбить схему на ярусы. При таком записывается выходная функция каждого элемента в предыдущем ярусе и подставляется на соответствующий вход на следующем ярусе. Этот анализа логических схем со всеми нюансами мы сегодня и рассмотрим.
3. B ∨ A
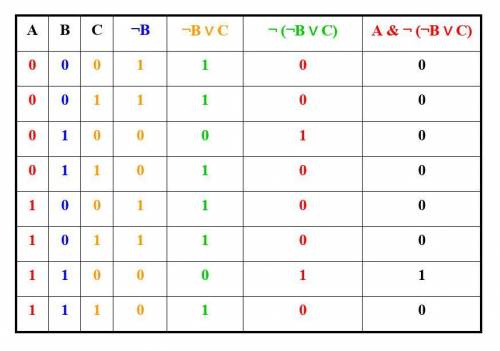
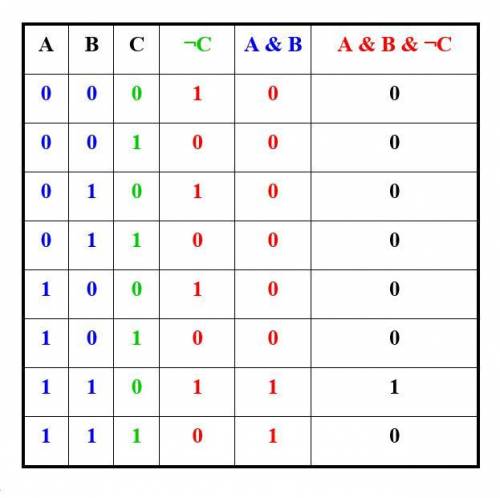
4. A & ¬(¬B ∨ C) ↔ A & B & ¬C (высказывания являются эквивалентными)
5. ложное
Объяснение:
3.
(¬A & B) ∨ (A & ¬B) ∨ (A & B) = (¬A & B) ∨ (A & B) ∨ (A & ¬B) = B & (¬A ∨ A) ∨ (A & ¬B) = B & 1 ∨ (A & ¬B) = B ∨ (A & ¬B) = (B ∨ A) & (B ∨ ¬B) = (B ∨ A) & 1 = B ∨ A
Согласно переместительному закону:
(¬A & B) ∨ (A & ¬B) ∨ (A & B) = (¬A & B) ∨ (A & B) ∨ (A & ¬B)
Согласно распределительному закону для логического сложения:
(¬A & B) ∨ (A & B) = B & (¬A ∨ A)
Согласно закону исключения третьего:
¬A ∨ A = 1
Согласно закону исключения констант для логического умножения:
B & 1 = B
Согласно распределительному закону для логического умножения:
B ∨ (A & ¬B) = (B ∨ A) & (B ∨ ¬B)
Согласно закону исключения третьего:
B ∨ ¬B = 1
Согласно закону исключения констант для логического умножения:
(B ∨ A) & 1 = B ∨ A
4.
A & ¬(¬B ∨ C) = A & ¬(¬B) & ¬C = A & B & ¬C
Согласно закону де Моргана:
¬(¬B ∨ C) = ¬(¬B) & ¬C
Согласно закону двойного отрицания:
¬(¬B) = B
A & ¬(¬B ∨ C) ↔ A & B & ¬C
(высказывания являются эквивалентными)
Составим таблицы истинности для доказательства эквивалентности (картинки)
5.
(¬(X < 5) ∨ (X < 3)) & (¬(X < 2) ∨ (X < 1)) при X = 1
Подставим значение X в высказывание, а затем определим истинность или ложность
(¬(1 < 5) ∨ (1 < 3)) & (¬(1 < 2) ∨ (1 < 1)) = (¬(истина) ∨ (истина)) & (¬(истина) ∨ (ложь)) = (ложь ∨ истина) & (ложь ∨ ложь) = истина & ложь = ложь
Общий порядок действий:
1) скобки
2) НЕ (¬, черта над выражением) - значение противоположно исходному высказыванию
3) И (&, ∧) - истинно, когда оба исходных высказывания истинны
4) ИЛИ (∨) - ложно, когда оба исходных высказывания ложны
85 98 84 17 84 43 42
Если из каждого кода вычесть 33, тоже ничего не поменяется. Значит, каждый код можно привести вычитаниями к промежутку 1..33:
19 32 18 17 18 10 9
Теперь каждый код — порядковый номер буквы в алфавите, и сообщение легко расшифровывается.
ответ: сюрприз