Давно, под влиянием книг Перельмана, Гарднера, Азимова и прочих, а также журналов вроде "Наука и жизнь" и "Квант", планировал на будущее писать собственные научно-популярные книги обо всем. Но к счастью вовремя понял, что бумажная литература в XXI веке - жанр не то чтобы вымирающий, но откровенно ретроградный, и в итоге переквалифицировался в блогеры. Многие посты из тех, что можно найти по тегу "занимательные бредни" (и не только) - это несостоявшиеся статьи/главы. Да, в ЖЖ есть свои "научпоперы" вроде sly2m'а с его физико-математической серией "На пальцах", и мои работы - полнейшая неихуровня ©, зато охват тем у меня поширше будет. Настолько, что даже сам не знаю, про что будет следующий пост.
Сейчас же, отсылаясь к первой главе гарднеровских "Математических досугов", хочу написать про латинские квадраты, конечные аффинные и проективные плоскости и обобщенно-круговые турниры. Что это за звери такие, как они связаны друг с другом и зачем это всё.
36.
Объяснение:
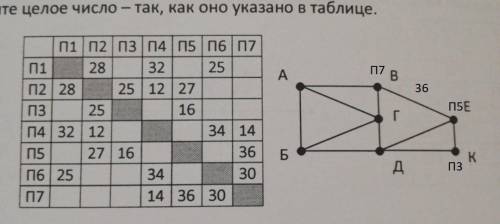
1. Ищем путь в таблице, который является уникальным, то есть отличается количеством путей. Таким пунктом является "П3", так как только у него есть два пути.
Ищем на схеме пункт с двумя путями. Это пункт "К". Отмечаем его, как "П3".
Итого получаем: "К" - "П3".
2. Смотрим какие пункты соединены с "П3". Это пункты "П2" и "П5".
У пункта "П2" 4 пути, у пункта "П5" 3 пути.
Ищем на схеме пункт, который связан с "К" и имеет 3 пути (берем именно три, так как нам нужно расстояние от В до Е, где В имеет три пути). Это пункт "Е". Отмечаем его, как "П5".
Итого получаем: "К" - "П3", "Е" - "П5".
3. Ищем в таблице пункт, который связан с "П5" и имеет три пути. "П2" не подходит, так как имеет 4 пути, "П3" мы уже соотнесли с "К". Подходит пункт "П7", так как он имеет три пути и связан с "П5". Соотнесем пункт "В" с "П7".
Итого получаем: "К" - "П3", "Е" - "П5", "В" - "П7".
Так как мы нашли пункты, которые соответствую В и Е, то можем найти расстояние между ними. В итоге, расстояние равно 36.
Если Маша тянет первая то она
Если Таня первая то моет Таня