3. 15
4. 4) ⌐A & ⌐B
Объяснение:
3.
y = 1 x = 11
пока условие x > 0 истинно (да) выполняется цикл
Действия в цикле:
1) x = x - 3
2) y = y + x
y = 1 x = 11
11 > 0 (да) выполняется цикл
Действия в цикле:
1) x = x - 3 = 11 - 3 = 8
2) y = y + x = 1 + 8 = 9
y = 9 x = 8
8 > 0 (да) выполняется цикл
Действия в цикле:
1) x = x - 3 = 8 - 3 = 5
2) y = y + x = 9 + 5 = 14
y = 14 x = 5
5 > 0 (да) выполняется цикл
Действия в цикле:
1) x = x - 3 = 5 - 3 = 2
2) y = y + x = 14 + 2 = 16
y = 16 x = 2
2 > 0 (да) выполняется цикл
Действия в цикле:
1) x = x - 3 = 2 - 3 = -1
2) y = y + x = 16 + (-1) = 16 - 1 = 15
y = 15 x = -1
-1 > 0 (нет) цикл не выполняется
y = 15 x = -1
4.
Составим таблицу истинности для каждого выражения (смотри картинку)
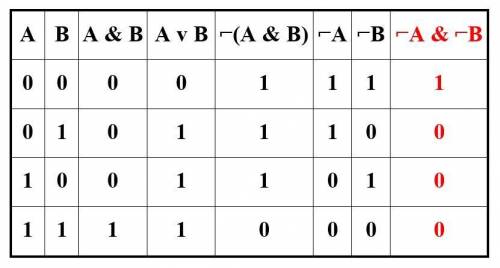
21
Объяснение:
y = 1 x = 10
пока условие x > 0 истинно (да) выполнить
Действия в цикле:
x = x - 2
y = y + x
y = 1 x = 10
10 > 0 (да)
Действия в цикле:
x = 10 - 2 = 8
y = 1 + 8 = 9
y = 9 x = 8
8 > 0 (да)
Действия в цикле:
x = 8 - 2 = 6
y = 9 + 6 = 15
y = 15 x = 6
6 > 0 (да)
Действия в цикле:
x = 6 - 2 = 4
y = 15 + 4 = 19
y = 19 x = 4
4 > 0 (да)
Действия в цикле:
x = 4 - 2 = 2
y = 19 + 2 = 21
y = 21 x = 2
2 > 0 (да)
Действия в цикле:
x = 2 - 2 = 0
y = 21 + 0 = 21
y = 21 x = 0
0 > 0 (нет)
Цикл не выполняется
Тема "Перевод из десятичной системы счисления в другие системы счисления"
Жил был художник в 7А316 году до нашей эры. И придумал он как-то раз нарисовать коллекцию сказочных картин о
жизни насекомых, которая состояла из 9E16 картин. Рисовал он, рисовал, и вдруг увидел 112 божьих коровки. Не
очень красивыми они ему показались. И решил он изменить цвет спинки, странно выглядела божья коровка.
Изменил у божьей коровки цвет головки, она опять странно выглядела. Сначала нарисовал художник 258 пятнышко
на спинке, а потом подумал он: 1516 пятнышек на одной божьей коровке - это очень много. Стер 168 пятнышек со
спинки - красивая она стала. И так ему божья коровка понравилась, что он нарисовал сразу 10012 штук. 10111112
картин художника повесили в музее, что бы все любовались. 1111112 картины художник подарил родителям и
близким друзьям. А у божьих коровок до сих пор точки на спине остались. Наверно до сих пор художник рисует. В
мире насчитываю более 76408 видов божьих коровок. Когда другие насекомые спрашивают: « Почему у вас божьих
коровок точки на спине?». Они отвечают: «Это нас художник раскрасил».