Уравнение реакции( один из вариантов):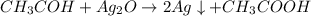
Чтобы расчитать выход продукта, нам нужно узнать сколько теоретически должно было выделиться продукта( "на бумаге").
Воспользуемся известной массой уксусного альдегида и найдём, сколько этого самого альдегида вступило в реакцию:
n( количество вещества) = m( масса) / M( молярная масса) - общая формула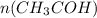
= 4,4 / 44= 0,1 моль
Из уравнения реакции видно, что коэффициент перед уксусным альдегидом равен коэффициенту перед уксусной кислотой, т.е.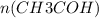 
= 
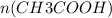= 0,1 моль
Теперь, пользуясь уже знакомой формулой n( количество вещества) = m( масса) / M( молярная масса), мы можем найти массу ( теоретическую) уксусной кислоты: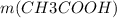
= 
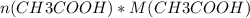= 0,1 * 60 = 6 г.
Выход продукта расчитываем по формуле:
w = m( практ) / m( теор) * 100% = 90%
ответ: выход продукта составил 90%.
Объяснение:
а) x² + 4x + 10 ≥ 0
D = 4² - 4· 10 = - 24
График функции у = x² + 4x + 10 - парабола веточками вверх, пересечения с осью Ох нет, т.к. D < 0, поэтому у > 0 и ответ
2) Решением неравенства является вся числовая прямая
b) -x² + 10x - 25 > 0
-(х - 5)² > 0
Поскольку -(х - 5)² < 0 при любых х, то ответ
1) Неравенство не имеет решений
c) x² + 3x + 2 ≤ 0
D = 3² - 4 · 2 = 1
x₁ = 0.5(-3 - 1) = -2
x₂ = 0.5(-3 + 1) = -1
График функции у = x² + 3x + 2 - парабола веточками вверх, пересекает ось Ох в точках с координатами x₁ = -2 и x₂ = -1 поэтому решением неравенства является интервал [-2; -1] , и ответ
4) Решением неравенства является закрытый промежуток.
d) -x² + 4 < 0
x² - 4 > 0
График функции у = x² - 4 - парабола веточками вверх, пересекает ось Ох в точках с координатами x₁ = -2 и x₂ = 2 поэтому решением неравенства является интервалы (-∞; -2) и (2; +∞) , и ответ
6) Решением неравенства является объединение двух промежутков.