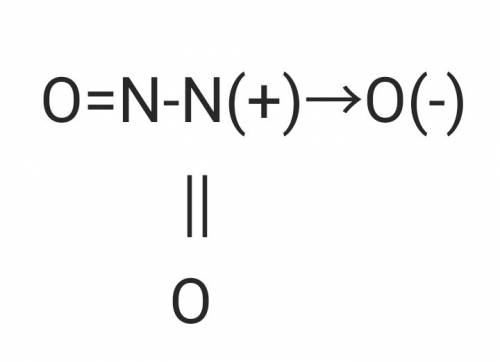
Объяснение:
1)Хоть у алюминия электропроводность ниже, чем у той-же меди, провода из него делать дешевле, поэтому его часто используют.
2) У сплавов алюминия большая ударная прочность.
4) Алюминий обладает хорошей пластичностью, из-за чего хорошо поддаётся обработке.
5) Из-за вышеописанной пластичности и небольшой стоимости.
6) Из-за высокой кислотности рассола алюминий начнёт окисляться, что может негативно сказаться на вкусовых качествах продукта
7) Алюминий не взаимодействует с концентрированными кислотами, только с разбавленными.
Основные приёмы, используемые при построении доказательств: прямое доказательство[⇨], математическая индукция и её обобщения[⇨], доказательство от противного[⇨], контрапозиция[⇨], построение[⇨], перебор[⇨], установление биекции[⇨], двойной счёт[⇨]; в приложениях в качестве математических доказательств привлекаются также методы, не дающие формального доказательства, но обеспечивающие практическую применимость результата[⇨] — вероятностные, статистические, приближённые. В зависимости от раздела математики, используемого формализма или математической школы не все методы могут приниматься безоговорочно, в частности, конструктивное доказательство[⇨] предполагает серьёзные ограничения.
Объяснение:
Основные приёмы, используемые при построении доказательств: прямое доказательство[⇨], математическая индукция и её обобщения[⇨], доказательство от противного[⇨], контрапозиция[⇨], построение[⇨], перебор[⇨], установление биекции[⇨], двойной счёт[⇨]; в приложениях в качестве математических доказательств привлекаются также методы, не дающие формального доказательства, но обеспечивающие практическую применимость результата[⇨] — вероятностные, статистические, приближённые. В зависимости от раздела математики, используемого формализма или математической школы не все методы могут приниматься безоговорочно, в частности, конструктивное доказательство[⇨] предполагает серьёзные ограничения.