Собственные числа находят из характеристического уравнения:
|A-λE|=0
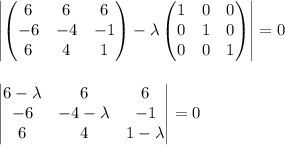
Проверяем будет ли -8 являться собственным числом данной матрицы:
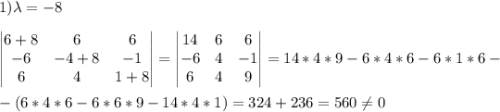
Определитель не равен нулю, следовательно -8 не является собственным числом матрицы А
Проверяем число 0
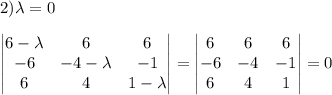
(вторая строка определителя пропорционально третьей строке, поэтому этот определитель равен нулю)
значит λ=0 - собственное число матрицы А
теперь находим собственный вектор из матричного уравнения:
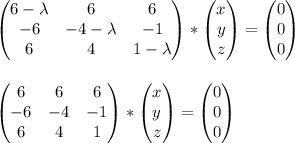
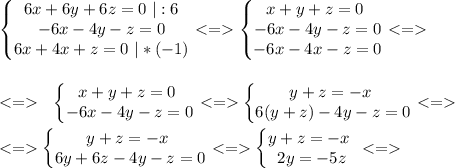
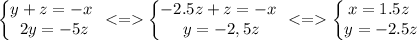
Собственный вектор будет иметь координаты:
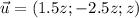
Пусть z=-2, тогда
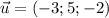
ответ: 5;-2
Периметр четвёртого = 14 (Он на столько же меньше большего, насколько средний больше меньшего)
А периметр ABCD = (11+14+16+19)/2 = 30
ответ: 30 см