Пошаговое объяснение:
S = πR² = πD²/4, где R - радиус, D - диаметр, D = 2R
S = 3,14 · 33,8²/4 = 896.8 (см²)
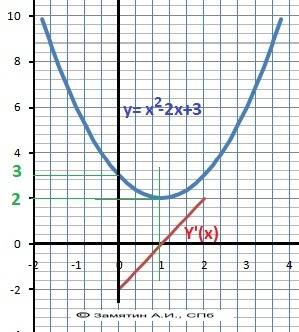
Дано: y = x² - 2x + 3
Исследование: (не очень интересная для исследования).
1. Область определения D(у) - Х∈(-∞;+∞) - непрерывная, гладкая.
2. Пересечение с осью Х. Находим корни уравнения.
Дискриминант D= -8. √48. Вещественных корней нет.
3. Поведение на бесконечности. limY(-∞) = - ∞ limY(+∞) = +∞
4. Интервалы знакопостоянства.
Y(x)> 0 - X∈(-∞;+∞) - во всём интервале определения.
3. Пересечение с осью У. У(0) = 3.
5. Исследование на чётность.Y(-x) = x² +2х+3 ≠ Y(x). Y(-x) ≠ -Y(x), Функция ни чётная ни нечётная.
6. Производная функции.Y'(x)= 2*Х - 2 = 2*(x - 1) = 0.
Корень при Х= 1.
7. Локальные экстремумы в корнях первой производной.
Минимум – Ymin(Х=1) = 2.
8. Интервалы возрастания и убывания.
Возрастает - Х∈(1;+∞), убывает = Х∈[Х₄; 1].
ВНИМАНИЕ на скобки - нет разрывов - квадратные скобки.
9. Вторая производная - Y"(x) = 2.
Корень производной - нет
10.
Вогнутая – "ложка" Х∈(-∞; +∞). - во всём интервале определения.
11. ВАЖНО: Асимптот - нет, ни вертикальных, ни горизонтальных, ни наклонных.
12. Область значений. E(y) - У∈ [2;+∞).
13. Рисунок к задаче с графиком в приложении.
Незнаю почему, но мне легче находить S и P при радиуса, диаметр – это 2 радиуса, значит:
S = πr²
2r = d
В задаче у нас указан диаметр, следовательно мы можем найти и радиус:
33,8 : 2 =16,9 - r
Дальше мы уже сможем найти площадь, если нам известен радиус и число ПИ:
S = 3,14 * 16,9²
S = 3,14 * 285, 61
S = 896, 8154
S = 897 см²