1.решите уравнение
1)х+36=83
х=83-36
х=47
2)124+у=212
х=212-124
х=88
3)а-458=345
а=345+458
а=803
4)2064-b=1398
b=2064-1398
b=666
2.решите уравнение
1) (х-34)+15=61
х-34+15=61
х-19=61
х=61+19
х=80
2) (к-36)-43=72
к-36-43=72
к-79=72
к=72+79
к=151
3) (37+b)-58=49
37+b-58=49
-21+b=49
b=49+21
b=70
4) 957-(t+336)=428
t+336=957-428
t+336=529
t=529-336
t=193
5) 325-(а-617)=219
325-(х-617)=219
х-617=325-219
х-617=106
х=106+617
х=723
6) 468-(259-с)=382
259-с=468-382
259-с=86
с=259-86
с=173
3.не решая уравнение (24-х)+37=49, установите,какое из чисел 19,7,12 является его корнем.
Подставим вместо Х значения
(24-19)+37=49,
5+37=49
42≠49 - 19 не корень
(24-7)+37=49,
17+37=49
54≠49 - 7 не корень
(24-12)+37=49,
12+37=49
49=49(и) - 12 корень
4. решите с уравнением задачу. Петя задумал число. если из этого числа вычесть 216 и полученную разность вычесть из 408, то получим 159. какое число задумал Петя.
Пусть Х - задуманное число
408-(х-216)=159
408-х+216=159
х=408+216-159,
х=465
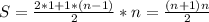
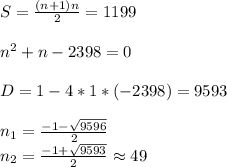
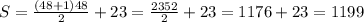
ax²+bx+c=0 - общий вид квадратичного уравнения
(х-2)(х+1)=(2х-5)²+1
х²+х-2х-2=4х²+25-20х+1
х²+х-2х-2-4х²-25+20х-1=0
-3х²+19х-28=0